
【题目】设函数![]() .
.
(1)求函数![]() 的单调区间和极值;
的单调区间和极值;
(2)若存在![]() 满足
满足![]() ,证明
,证明![]() 成立.
成立.
【答案】(1)当![]() 时,
时, ![]() 在
在![]() 上单调递增没有极值;当
上单调递增没有极值;当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() 在
在![]() 上单调递减,极小值为
上单调递减,极小值为![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)对函数进行求导得![]() ,分为
,分为![]() 和
和![]() 两种情形判别导数与0的关系即可得结果;
两种情形判别导数与0的关系即可得结果;
(2)先得出![]() ,结合(1)知
,结合(1)知![]() ,设
,设![]() ,构造函数
,构造函数![]() ,通过导数判断出
,通过导数判断出![]() 的单调性,可得出
的单调性,可得出![]() ,结合(1)中的单调性即可得出结果.
,结合(1)中的单调性即可得出结果.
(1)由![]() 得
得![]()
当![]() 时,
时,![]() 从而得
从而得![]() 在
在![]() 上单调递增没有极值;
上单调递增没有极值;
当![]() 时,
时,![]() 得
得![]() ;
;
![]() 得
得![]() ;
;![]() 得
得![]() ;
;
![]() 在
在![]() 上单调递增,
上单调递增,![]() 在
在![]() 上单调递减,
上单调递减,
此时有极小值![]() ,无极大值.
,无极大值.
(2)由![]() 得:
得:![]() ,从而得
,从而得![]()
由(1)知当![]() 时,
时,![]() 从而得
从而得![]() 在
在![]() 上单调递增,所以此时不成立
上单调递增,所以此时不成立
可知此时![]() ,由于
,由于![]() 的极小值点为
的极小值点为![]() ,可设
,可设![]()
设![]()
![]()
![]()
![]() ,仅当
,仅当![]() 时取得“
时取得“![]() ”
”
所以![]() 在
在![]() 为单调递增函数且
为单调递增函数且![]()
当![]() ,时有
,时有![]() ,即
,即![]()
又由![]() ,所以
,所以![]()
又由(1)知![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,
,![]()
所以![]() 从而得证
从而得证![]() 成立.
成立.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】两城市![]() 和
和![]() 相距
相距![]() ,现计划在两城市外以
,现计划在两城市外以![]() 为直径的半圆
为直径的半圆![]() 上选择一点
上选择一点![]() 建造垃圾处理场,其对城市的影响度与所选地点到城市的距离有关,对城
建造垃圾处理场,其对城市的影响度与所选地点到城市的距离有关,对城![]() 和城
和城![]() 的总影响度为城
的总影响度为城![]() 和城
和城![]() 的影响度之和,记
的影响度之和,记![]() 点到城
点到城![]() 的距离为
的距离为![]() ,建在
,建在![]() 处的垃圾处理场对城
处的垃圾处理场对城![]() 和城
和城![]() 的总影响度为
的总影响度为![]() ,统计调查表明:垃圾处理场对城
,统计调查表明:垃圾处理场对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比,比例系数为4,对城
的距离的平方成反比,比例系数为4,对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比,比例系数为
的距离的平方成反比,比例系数为![]() ,当垃圾处理场建在
,当垃圾处理场建在![]() 的中点时,对城
的中点时,对城![]() 和城
和城![]() 的总影响度为0.065;
的总影响度为0.065;
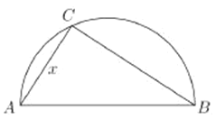
(1)将![]() 表示成
表示成![]() 的函数;
的函数;
(2)判断![]() 上是否存在一点,使建在此处的垃圾处理场对城
上是否存在一点,使建在此处的垃圾处理场对城![]() 和城
和城![]() 的总影响度最小?若存在,求出该点到城
的总影响度最小?若存在,求出该点到城![]() 的距离;若不存在,说明理由;
的距离;若不存在,说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1000辆.本年度为适应市场需求,计划提高产品档次,适度增加投入成本.若每辆车投入成本增加的比例为x(0<x<1),则出厂价相应的提高比例为0.75x,同时预计年销售量增加的比例为0.6x.已知年利润=(出厂价﹣投入成本)×年销售量.
(1)写出本年度预计的年利润y与投入成本增加的比例x的关系式;
(2)为使本年度的年利润比上年有所增加,问投入成本增加的比例x应在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数对序列![]() 、
、![]() 、
、![]() 、
、![]() ,记
,记![]() ,
,![]() ,其中
,其中![]() 表示
表示![]() 和
和![]() 两个数中最大的数.
两个数中最大的数.
(1)对于数对序列![]() ,
,![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)记![]() 为
为![]() 、
、![]() 、
、![]() 、
、![]() 四个数中最小值,对于由两个数对
四个数中最小值,对于由两个数对![]() 、
、![]() 组成的数对序列
组成的数对序列![]() 、
、![]() 和
和![]() 、
、![]() ,试分别对
,试分别对![]() 和
和![]() 的两种情况比较
的两种情况比较![]() 和
和![]() 的大小;
的大小;
(3)在由![]() 个数对
个数对![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 组成的所有数对序列中,写出一个数对序列
组成的所有数对序列中,写出一个数对序列![]() 使
使![]() 最小,并写出
最小,并写出![]() 的值.(只需写出结论)
的值.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知曲线![]() ,曲线
,曲线![]() ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与![]() 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.
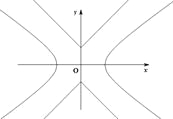
(1)在正确证明![]() 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线![]() 与
与![]() 有公共点,求证
有公共点,求证![]() ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;
(3)求证:圆![]() 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)若![]() ,求曲线
,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com