
已知数列 的前n项和为
的前n项和为 ,
, ,且
,且 (
( ),数列
),数列 满足
满足 ,
, ,对任意
,对任意 ,都有
,都有 .
.
(Ⅰ)求数列 、
、 的通项公式;
的通项公式;
(Ⅱ)令 ,若对任意的
,若对任意的 ,不等式
,不等式 恒成立,试求实数λ的取值范围.
恒成立,试求实数λ的取值范围.
(Ⅰ)∵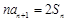 ,∴
,∴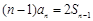 (
(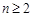 ),两式相减得,
),两式相减得,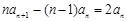 ,
,
∴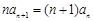 ,即
,即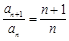 ,∴
,∴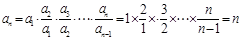 (
(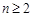 ),
),
 满足上式,故数列
满足上式,故数列 的通项公式
的通项公式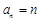 (
(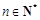 ).··········· 4分
).··········· 4分
在数列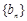 中,由
中,由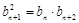 ,知数列
,知数列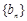 是等比数列,首项、公比均为
是等比数列,首项、公比均为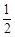 ,
,
∴数列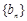 的通项公式.(若列出
的通项公式.(若列出 、
、 、
、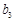 直接得
直接得 而没有证明扣1分)···· 6分
而没有证明扣1分)···· 6分
(Ⅱ)∴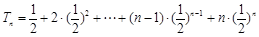 ①
①
∴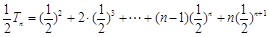 ②
②
由①-②,得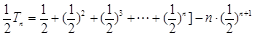
 ,
,
∴ ,·························· 8分
,·························· 8分
不等式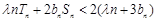 即为
即为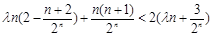 ,
,
即 (
(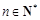 )恒成立.··············· 9分
)恒成立.··············· 9分
方法一、设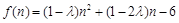 (
(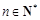 ),
),
当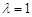 时,
时, 恒成立,则
恒成立,则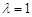 满足条件;
满足条件;
当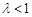 时,由二次函数性质知不恒成立;
时,由二次函数性质知不恒成立;
当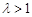 时,
由于
时,
由于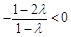 ,则
,则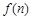 在
在 上单调递减,
上单调递减, 恒成立,则
恒成立,则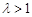 满足条件.
满足条件.
综上所述,实数λ的取值范围是 .··············· 12分
.··············· 12分
方法二、也即 (
(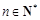 )恒成立,·············· 9分
)恒成立,·············· 9分
令 .则
.则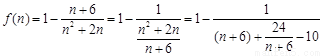 ,·· 10分
,·· 10分
由 ,
, 单调递增且大于0,∴
单调递增且大于0,∴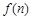 单调递增,当
单调递增,当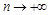 时,
时, ,且
,且 ,故
,故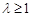 ,∴实数λ的取值范围是
,∴实数λ的取值范围是 .
.
【解析】略


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| bnbn+1 |
查看答案和解析>>
科目:高中数学 来源:2012届福建省高二下学期期末考试数学(文) 题型:解答题
(12分)已知数列 的前n项和为
的前n项和为 ,
, 且满足
且满足 =2
=2 +n (n>1且n∈
+n (n>1且n∈ )
)
(1)求数列 的通项公式和前n项的和
的通项公式和前n项的和
(2)设 ,求使得不等式
,求使得不等式 成立的最小正整数n的值
成立的最小正整数n的值
查看答案和解析>>
科目:高中数学 来源:陕西省汉台区2009-2010学年高二第二学期期末考试(数学文)doc 题型:解答题
(本小题满分14分)
已知数列 的前n项和为
的前n项和为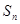 ,且
,且 ,
,
(1)试计算 ,并猜想
,并猜想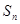 的表达式;
的表达式;
(2) 证明你的猜想,并求出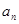 的表达式。
的表达式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com