
 、
、 的每一项都是正数,
的每一项都是正数, ,
, ,且
,且 、
、 、
、 成等差数列,
成等差数列, 、
、 、
、 成等比数列,
成等比数列, .
.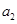 、
、 的值;
的值; 、
、 的通项公式;
的通项公式; ,有
,有 .
.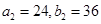 ;(Ⅱ)
;(Ⅱ)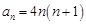 ,
,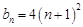 ;(Ⅲ)答案详见解析.
;(Ⅲ)答案详见解析.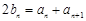 ,
,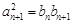 ,并结合已知
,并结合已知 ,
, ,利用赋值法可求
,利用赋值法可求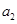 、
、 的值;(Ⅱ)由
的值;(Ⅱ)由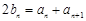 ①,
①,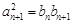 ②,且
②,且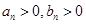 ,则
,则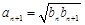 ,
,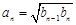 (
(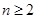 ),代入①中,得关于
),代入①中,得关于 的递推公式
的递推公式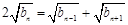 ,故可判断数列
,故可判断数列 是等差数列,从而可求出
是等差数列,从而可求出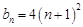 ,代入
,代入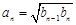 (
(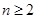 )中,求出
)中,求出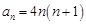 (
(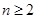 ),再检验
),再检验 时,
时,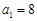 是否满足,从而求出
是否满足,从而求出 ;(Ⅲ)和式
;(Ⅲ)和式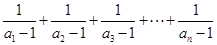 相当于数列
相当于数列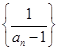 的前
的前 项和,先确定其通项公式,根据通项公式的不同形式,选择相应的求和方法,先求得
项和,先确定其通项公式,根据通项公式的不同形式,选择相应的求和方法,先求得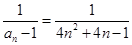 ,不易求和,故可考虑放缩法,将其转化为容易求和的形式,再证明和小于
,不易求和,故可考虑放缩法,将其转化为容易求和的形式,再证明和小于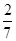 .
.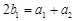 ,可得
,可得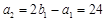 ,由
,由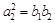 ,可得
,可得 .
. 、
、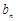 、
、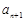 成等差数列,所以
成等差数列,所以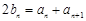 …①.因为
…①.因为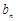 、
、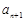 、
、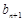 成等比数列,所以
成等比数列,所以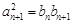 ,因为数列
,因为数列 、
、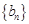 的每一项都是正数,所以
的每一项都是正数,所以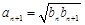 …②.于是当
…②.于是当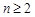 时,
时,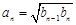 …③.将②、③代入①式,可得
…③.将②、③代入①式,可得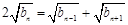 ,因此数列
,因此数列 是首项为4,公差为2的等差数列,所以
是首项为4,公差为2的等差数列,所以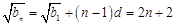 ,于是
,于是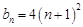 .由③式,可得当
.由③式,可得当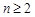 时,
时,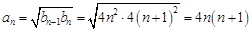 .当
.当 时,
时,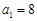 ,满足该式子,所以对一切正整数
,满足该式子,所以对一切正整数 ,都有
,都有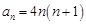 .
.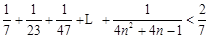 .
.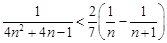 (
(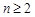 ).
).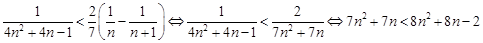
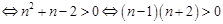 ,
,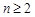 时,
时,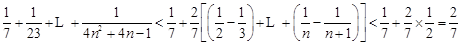 .
.  时,
时,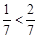 .
. ,有
,有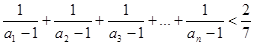
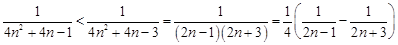 .
.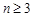 时,
时,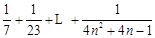

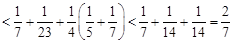 .
. 时,
时,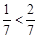 ;当
;当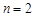 时,
时,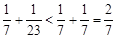 .
. ,有
,有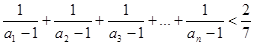
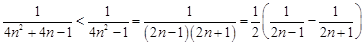 .当
.当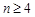 时,
时,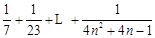
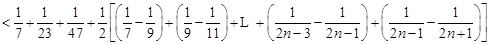
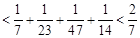 .
. 时,
时,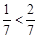 ;当
;当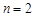 时,
时,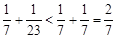 ;当
;当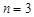 时,
时,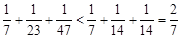 .
. ,有
,有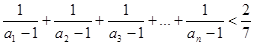


科目:高中数学 来源:不详 题型:解答题
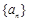 的前
的前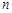 项和为
项和为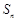 ,已知
,已知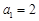 ,
, .
.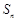 ;
;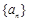 中抽取一个公比为
中抽取一个公比为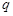 的等比数列
的等比数列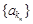 ,其中
,其中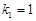 ,且
,且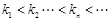 ,
,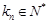 .
.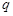 取最小值时,求
取最小值时,求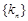 的通项公式;
的通项公式;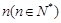 的不等式
的不等式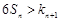 有解,试求
有解,试求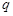 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 满足
满足 ,
, ,
, ,
, 是数列
是数列 的前
的前 项和.
项和. 为等差数列.
为等差数列. ;
; 满足
满足 ,数列
,数列 满足
满足 ,试比较数列
,试比较数列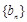 前
前 项和
项和 与
与 前
前 项和
项和 的大小;
的大小; ,
,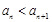 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,Sn为数列{an}的前n项和,则S8= ;S4n= 。
,Sn为数列{an}的前n项和,则S8= ;S4n= 。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com