练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．在△ABC中，角A，B，C所对的边分别是a，b，c．若a=3bsinC且cosA=3cosBcosC，则tanA的值为（　　）
    A．4B．-4C．-3D．3

    分析 运用正弦定理，把边化成角得到sinA=3sinBsinC，再与条件cosA=3cosBcosC相减，运用两角和的余弦公式，再用诱导公式转化为cosA，由同角公式，即可求出tanA．

    解答 解：∵a=3bsinC，
    由正弦定理得：sinA=3sinBsinC①，
    又cosA=3cosBcosC②，
    ②-①得，cosA-sinA=3（cosBcosC-sinBsinC）
    =3cos（B+C）=-3cosA，
    ∴sinA=4cosA，
    ∴tanA=$\frac{sinA}{cosA}$=4．
    故选：A．

    点评 本题主要考查解三角形中的正弦定理及应用，同时考查两角和差的余弦公式，诱导公式，以及同角三角函数的关系式，这些都是三角中的基本公式，务必要掌握，注意公式的逆用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    5．函数f（x）=ln$\frac{{e}^{x}-1}{x}$，数列{an}满足a1=1，an+1=f（an）．
    （1）试求f（x）的单调区间；
    （2）求证：数列{an}为递减数列，且an＞0恒成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．过椭圆$\frac{y^2}{4}+{x^2}=1$的上焦点F2作一条斜率为-2的直线与椭圆交于A，B两点，则|AB|=$\frac{5}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．过正方体ABCD-A1B1C1D1的顶点A作直线，使与直线AD1所成的角为30°，且与平面C1D1C所成的角为60°，则这样的直线的条数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

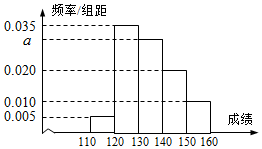    10．从高三年级随机抽取200名学生，将他们的某次考试数学成绩绘制成频率分布直方图．由图中数据可知成绩在[130，140）内的学生人数为60．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=x2-2alnx，（a∈R）．
    （1）求函数f（x）的单调区间；
    （2）当方程f（x）=2ax有唯一解时，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知集合A={（x，y）|y=3x-2}，B={（x，y）|y=x}那么集合A∩B={（1，1）}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．等差数列的第5项a5=8，且a1+a2+a3=6，则d=（　　）
    A．3B．-3C．2D．-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知点P是△ABC的中位线EF上任意一点，且EF∥BC，实数x，y满足$\overrightarrow{PA}+x\overrightarrow{PB}+y\overrightarrow{PC}=\overrightarrow 0$，设△ABC，△PBC，△PCA，△PAB的面积分别为S，S1，S2，S3，记$\frac{S_1}{S}={λ_1}$，$\frac{S_2}{S}={λ_2}$，$\frac{S_3}{S}={λ_3}$，则λ2•λ3取最大值时，3x+y的值为（　　）
    A．$\frac{1}{2}$B．$\frac{3}{2}$C．1D．2

    查看答案和解析>>

    同步练习册答案