练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知实数x，y满足
    2x-y≥0
    2x+y≥0
    x≤3
    ，则z=x-2y的最小值是
    -9
    -9
    ．
    分析：先画出满足约束条件：
    2x-y≥0
    2x+y≥0
    x≤3
    ，的平面区域，求出平面区域的各角点，然后将角点坐标代入目标函数，比较后，即可得到目标函数z=x-2y的最小值．
    解答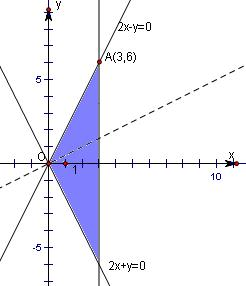：解：根据题意，画出可行域与目标函数线如下图所示，
    由图可知目标函数z=x-2y在点A（3，6）取最小值-9．
    故答案为：-9．
    点评：用图解法解决线性规划问题时，分析题目的已知条件，找出约束条件和目标函数是关键，可先将题目中的量分类、列出表格，厘清头绪，然后列出不等式组（方程组）寻求约束条件，并就题目所述找出目标函数．然后将可行域各角点的值一一代入，最后比较，即可得到目标函数的最优解．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知实数x、y满足
    (2-
    		3
    )x+y-6+2
    		3
    ≤0
    2x-y-2＞0
    y-
    		3
    ≥0
    ，则
    xy
    (x-y)(x+y)
    的取值范围是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知实数x，y满足x2+y2-4x+6y+12=0，则|2x-y-2|的最小值是（　　）
    A、5-
    		5
    B、4-
    		5
    C、5
    D、4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•广东模拟）已知实数x，y满足约束条件
    x≥1
    y≤1
    x-y≤0
    ’则z=2x-y的取值范围是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知实数x，y满足：
    x-y+2≥0
    y≥
    1
    2
    x+1
    x+y-1≥0
    ，则目标函数z=2x-y（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知实数x，y满足
    x-2y≤0
    x+y-3≥0
    0≤y≤2
    ，则z=(
    1
    2
    )x•(
    1
    4
    )y    的最大值为
     
    ．

    查看答案和解析>>

    同步练习册答案