
分析 (I)由已知中椭圆通径的端点坐标,构造方程组,可得a,b的值,进而可得椭圆C的方程;
(II)经过点P(1,0)的直线l可设为x=my+1,
(i)设A(x1,y1),B(x2,y2),联立直线与椭圆的方程,结合韦达定理,可得y1+y2=$\frac{-2m}{{m}^{2}+4}$,y1y2=$\frac{-3}{{m}^{2}+4}$,由椭圆的右顶点为E(2,0),可得:k1•k2=$\frac{{y}_{1}}{{x}_{1}-2}$•$\frac{{y}_{2}}{{x}_{2}-2}$=$\frac{{y}_{1}•{y}_{2}}{({my}_{1}-1)({my}_{2}-1)}$=$\frac{{y}_{1}•{y}_{2}}{{{m}^{2}y}_{1}•{y}_{2}-{m({y}_{1}+y}_{2})+1}$,进而得到答案;
(ii)利用点差法,可得kAB=-$\frac{1}{4}$•$\frac{{x}_{0}}{{y}_{0}}$,故直线l的垂直平分线方程为:y-y0=$\frac{{y}_{0}}{4{x}_{0}}$(x-x0),令y=0,得P点横坐标,结合由H(x0,y0)在椭圆内部,可得答案.
解答 解:(I)由已知中过F1于x轴垂直的直线与椭圆C相交,其中一个交点为M(-$\sqrt{3}$,$\frac{1}{2}$).
可得:c=$\sqrt{3}$,$\frac{{b}^{2}}{a}$=$\frac{1}{2}$,a2-b2=c2,
解得:a=2,b=1,
∴椭圆C的方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$;…3分
(II)设A(x1,y1),B(x2,y2)
证明:(i)∵直线l过定点(1,0),设x=my+1,
由$\left\{\begin{array}{l}\frac{{x}^{2}}{4}+{y}^{2}=1\\ x=my+1\end{array}\right.$得:(m2+4)y2+2my-3=0,…5分
∴y1+y2=$\frac{-2m}{{m}^{2}+4}$,y1y2=$\frac{-3}{{m}^{2}+4}$,
∵右顶点为E(2,0),
∴k1•k2=$\frac{{y}_{1}}{{x}_{1}-2}$•$\frac{{y}_{2}}{{x}_{2}-2}$=$\frac{{y}_{1}•{y}_{2}}{({my}_{1}-1)({my}_{2}-1)}$=$\frac{{y}_{1}•{y}_{2}}{{{m}^{2}y}_{1}•{y}_{2}-{m({y}_{1}+y}_{2})+1}$=$\frac{\frac{-3}{{m}^{2}+4}}{{{m}^{2}•\frac{-3}{{m}^{2}+4}}_{1}-m•\frac{-2m}{{m}^{2}+4}+1}$=-$\frac{3}{4}$,
∴k1•k2为定值;…8分
(ii)将A(x1,y1),B(x2,y2)代入椭圆方程得:$\left\{\begin{array}{l}\frac{{{x}_{1}}^{2}}{4}+{{y}_{1}}^{2}=1\\ \frac{{{x}_{2}}^{2}}{4}+{{y}_{2}}^{2}=1\end{array}\right.$,
两式相减得:$\frac{1}{4}$(x1-x2)(x1+x2)=-(y1-y2)(y1+y2)
∵直线l的垂直平分线与x轴交于一点P,
∴y1+y2≠0,x1-x2≠0,
∴-$\frac{1}{4}$•$\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}$=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=kAB,
设AB的中点H(x0,y0),则kAB=-$\frac{1}{4}$•$\frac{{x}_{0}}{{y}_{0}}$,
故直线l的垂直平分线方程为:y-y0=$\frac{{y}_{0}}{4{x}_{0}}$(x-x0),
令y=0,得P点横坐标为:$\frac{3}{4}{x}_{0}$…10分,
由H(x0,y0)在椭圆内部,可得:x0∈(-2,2),
故$\frac{3}{4}{x}_{0}$∈(-$\frac{3}{2}$,$\frac{3}{2}$)…12分
点评 本题考查的知识点是椭圆的方程,椭圆的性质,直线与椭圆的位置关系,难度中档.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
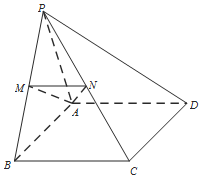 在四棱锥P-ABCD中,△PAB为正三角形,四边形ABCD为矩形,平面PAB⊥平面ABCD,AB=2AD,M,N分别为PB,PC中点.
在四棱锥P-ABCD中,△PAB为正三角形,四边形ABCD为矩形,平面PAB⊥平面ABCD,AB=2AD,M,N分别为PB,PC中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{11}$ | C. | -$\frac{1}{13}$ | D. | -$\frac{1}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com