
如图所示,四边形ABCD是边长为2的正方形,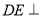 平面ABCD,AF//DE,DE=2AF,BE与平面ABCD所成角的正切值为
平面ABCD,AF//DE,DE=2AF,BE与平面ABCD所成角的正切值为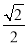 .
.
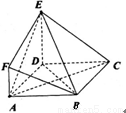
(1)求证:AC//平面EFB;
(2)求二面角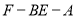 的大小.
的大小.
(1)见解析;(2)二面角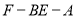 的大小为
的大小为 .
.
【解析】
试题分析:(1)设AC、BD交于O,取EB的中点G.连结FG,GO.
在△BDE中,OG∥DE且OG=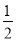 DE,FA∥DE且FA=
DE,FA∥DE且FA=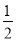 DE,∴OG∥FA且OG=FA,
DE,∴OG∥FA且OG=FA,
∴四边形FAOG为平行四边形. 2分
∴FG∥AO,又AG 平面EFB,FG
平面EFB,FG 平面EFB,
平面EFB,
∴直线AC∥平面EFB; 4分
(2)∵DE⊥平面ABCD,∴BE与平面ABCD所成角就是∠DBE.
又BE与平面ABCD所成的角的正切值为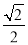 ,∴
,∴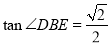 ,而BD=
,而BD=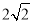 ,∴DE=2. 6分
,∴DE=2. 6分
分别以DA、DC、DE所在的直线为x,y,z轴,建立空间直角坐标系D-xyz,则有A(2,0,0),B(2,2,0),E(0,0,2),F(2,0,1),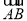 =(0,2,0),
=(0,2,0),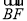 =(0,-2,1),
=(0,-2,1),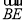 =(-2,-2,2),
=(-2,-2,2),
设平面AEB的法向量为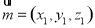 ,则
,则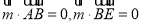 ,即
,即 ,
,
令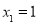 ,可得
,可得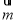 =(1,0,1), 9分
=(1,0,1), 9分
设平面FBE的法向量为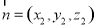 ,
, ,则
,则 ,
,
令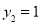 ,可得
,可得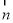 =(1,1,2), 11分
=(1,1,2), 11分
设二面角F-BE-A的大小为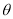 ,
,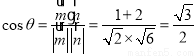 ,
,
∴二面角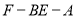 的大小为
的大小为 . 12分
. 12分
考点:考查了直线与平面平行的判定,二面角的大小.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014-2015学年山东省烟台市高三期末考试理科数学试卷(解析版) 题型:选择题
6.某次数学摸底考试共有10道选择题,每道题四个选项中有且只有一个选项是正确的;张三同学每道题都随意地从中选了一个答案,记该同学至少答对9道题的概率为P,则下列数据中与P的值最接近的是
A. B.
B.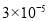 C.
C.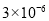 D.
D.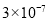
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省韶关市高三调研考试文科数学试卷(解析版) 题型:选择题
记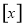 表示不超过
表示不超过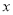 的最大整数,例如
的最大整数,例如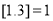 ,
,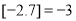 .函数
.函数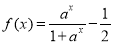
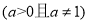 ,在
,在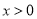 时恒有
时恒有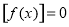 ,则实数
,则实数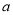 的取值范围是( )
的取值范围是( )
A.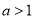 B.
B.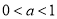 C.
C.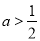 D.
D.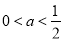
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com