
【题目】已知函数![]() 在区间
在区间![]() 上的最大值为4,最小值为1.
上的最大值为4,最小值为1.
(1)求实数![]() 、
、![]() 的值;
的值;
(2)记![]() ,若
,若![]() 在
在![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)对于函数![]() ,用
,用![]() ,1,2,
,1,2,![]() ,
,![]() ,
,![]() 将区间
将区间![]() 任意划分成
任意划分成![]() 个小区间,若存在常数
个小区间,若存在常数![]() ,使得和式
,使得和式![]() 对任意的划分恒成立,则称函数
对任意的划分恒成立,则称函数![]() 为
为![]() 上的有界变差函数.记
上的有界变差函数.记![]() ,试判断函数
,试判断函数![]() 是否为在
是否为在![]() 上的有界变差函数?若是,求
上的有界变差函数?若是,求![]() 的最小值;若不是,请说明理由.
的最小值;若不是,请说明理由.
(参考公式:![]()
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)是,6.
;(3)是,6.
【解析】
(1)由已知中![]() 在区间
在区间![]() 的最大值为4,最小值为1,结合函数的单调性及最值,构造出关于
的最大值为4,最小值为1,结合函数的单调性及最值,构造出关于![]() ,
,![]() 的方程组,解得
的方程组,解得![]() ,
,![]() 的值;
的值;
(2)由![]() 的解析式可得
的解析式可得![]() 的解析式,讨论
的解析式,讨论![]() 的符号结合对勾函数的图象和单调性可得
的符号结合对勾函数的图象和单调性可得![]() 的范围;
的范围;
(3)根据有界变差函数的定义,我们先将区间![]() 进行划分,进而判断
进行划分,进而判断![]() 是否恒成立,进而得到结论.
是否恒成立,进而得到结论.
(1)![]() 函数
函数![]() ,因为
,因为![]() ,
,
所以![]() 在区间
在区间![]() 上是增函数,
上是增函数,
又![]() 函数
函数![]() 故在区间
故在区间![]() ,
,![]() 上的最大值为4,最小值为1,
上的最大值为4,最小值为1,
![]() ,即
,即![]() ,
,
解得![]() ,
,![]() ;
;
(2)由已知可得![]() ,
,
![]() ,
,
若![]() 在
在![]() 上是单调函数,
上是单调函数,
若![]() ,即
,即![]() ,由两个增函数的和还是增函数,易得函数
,由两个增函数的和还是增函数,易得函数![]() 在
在![]() 递增;
递增;
若![]() ,函数
,函数![]() 为对勾函数,结合图象可知:在
为对勾函数,结合图象可知:在![]() 递增;
递增;
![]() 或
或![]() ,解得:
,解得:![]() 或
或![]() .
.
综上所述:![]() 或
或![]() .
.
(3)函数![]() 为
为![]() 上的有界变差函数.
上的有界变差函数.
因为函数![]() 为
为![]() 递增,
递增,![]() 递减,
递减,![]() 上的单调递增函数,
上的单调递增函数,
且对任意划分![]() ,
,
有![]()
![]()
![]()
![]() 恒成立,①
恒成立,①
且对任意划分![]() ,
,
有![]() ,
,
![]()
![]()
![]() 恒成立,②
恒成立,②
且对任意划分![]() ,
,
有![]()
![]() ,
,
![]()
![]()
![]() 恒成立,③
恒成立,③
![]() 由①②③可得
由①②③可得![]() ,
,
![]() 存在常数
存在常数![]() ,使得
,使得![]() 恒成立,
恒成立,![]() 的最小值为6.
的最小值为6.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
(I)估计顾客同时购买乙和丙的概率;
(II)估计顾客在甲、乙、丙、丁中同时购买3中商品的概率;
(III)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)在直角坐标系xOy中,直线l的参数方程为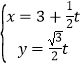 (t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,
(t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,![]() c的极坐标方程为
c的极坐标方程为![]() =2
=2![]() sin
sin![]() .
.
(1)写出![]() c的直角坐标方程;
c的直角坐标方程;
(2)P为直线l上一动点,当P到圆心C的距离最小时,求P的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若将函数y=2sin 2x的图像向左平移 ![]() 个单位长度,则评议后图象的对称轴为( )
个单位长度,则评议后图象的对称轴为( )
A.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
B.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
C.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
D.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选修4﹣1:几何证明选讲)
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于D.
(1)证明:DB=DC;
(2)设圆的半径为1,BC= ![]() ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已成椭圆 ![]() 的左右顶点分别为
的左右顶点分别为 ![]() ,上下顶点分别为
,上下顶点分别为 ![]() ,左右焦点分别为
,左右焦点分别为 ![]() ,其中长轴长为4,且圆
,其中长轴长为4,且圆 ![]() 为菱形
为菱形 ![]() 的内切圆.
的内切圆.
(1)求椭圆 ![]() 的方程;
的方程;
(2)点 ![]() 为
为 ![]() 轴正半轴上一点,过点
轴正半轴上一点,过点 ![]() 作椭圆
作椭圆 ![]() 的切线
的切线 ![]() ,记右焦点
,记右焦点 ![]() 在
在 ![]() 上的射影为
上的射影为 ![]() ,若
,若 ![]() 的面积不小于
的面积不小于 ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)在其图像上存在不同的两点A(x1 , y1),B(x2 , y2),其坐标满足条件:|x1x2+y1y2|﹣ ![]() 的最大值为0,则称f(x)为“柯西函数”, 则下列函数:
的最大值为0,则称f(x)为“柯西函数”, 则下列函数:
①f(x)=x+ ![]() (x>0);
(x>0);
②f(x)=lnx(0<x<3);
③f(x)=2sinx;
④f(x)= ![]() .
.
其中为“柯西函数”的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点 (Ⅰ)求证:平面PAB⊥平面CDE;
(Ⅱ)若直线PC与平面PAD所成角为45°,求二面角A﹣DE﹣C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com