
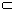
(Ⅰ)证明PA//平面EDB;
(Ⅱ)证明PB⊥平面EFD;
(Ⅲ)求二面角C-PB-D的大小.
19. 本小题考查直线与平面平行,直线与平面垂直、二面角等基础知识,考查空间想象能力和推理论证能力.
方法一:
(Ⅰ)证明:连结AC,AC交BD于O.连结EO.
∵底面ABCD是正方形,∴点O是AC的中点.
在△PAC中,EO是中位线,∴PA∥EO.
而EO![]() 平面EDB且PA
平面EDB且PA![]() 平面EDB,
平面EDB,
所以,PA∥平面EDB.
(Ⅱ)证明:∵PD⊥底面ABCD且DC![]() 底面ABCD,∴PD⊥DC.
底面ABCD,∴PD⊥DC.
∵PD=DC,可知△PDC是等腰直角三角形,而DE是斜边PC的中线,
∴DE⊥PC. ①
同样由PD⊥底面ABCD,得PD⊥BC.
∵底面ABCD是正方形,有DC⊥BC,
∴BC⊥平面PDC.
而DE![]() 平面PDC,∴BC⊥DE. ②
平面PDC,∴BC⊥DE. ②
由①和②推得DE⊥平面PBC.
而PB![]() 平面PBC,∴DE⊥PB.
平面PBC,∴DE⊥PB.
又EF⊥PB且DE∩EF=E,所以PB⊥平面EFD.
(Ⅲ)解:由(Ⅱ)知PB⊥DF,故∠EFD是二面角C-PB-D的平面角.
由(Ⅱ)知,DE⊥EF,PD⊥DB.
设正方形ABCD的边长为a,则PD=DC=a,BD=![]() a,
a,
PB=![]() =
=![]() a,
a,
PC=![]() =
=![]() a,
a,
DE=![]() PC=
PC=![]() a.
a.
在Rt△PDB中,
DF=![]() =
=![]() =
=![]() a.
a.
在Rt△EFD中,
sinEFD=![]() =
=![]() =
=![]() ,∴∠EFD=
,∴∠EFD=![]() .
.
所以,二面角C-PB-D的大小为![]() .
.
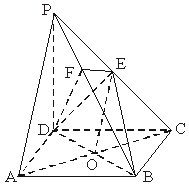
方法二:如图所示建立空间直角坐标系,D为坐标原点.设DC=a.
(Ⅰ)证明:连结AC,AC交BD于G.连结EG.
依题意得A(a,0,0),P(0,0,a),E(0,![]() ,
, ![]() ).
).
∵底面ABCD是正方形,∴G是此正方形的中心,故点G的坐标为(![]() ,
,![]() ,0)且
,0)且
![]() =(a,0,-a),
=(a,0,-a),![]() =(
=( ![]() ,0,-
,0,-![]() ).
).
∴![]() =2
=2![]() .这表明PA∥EG.
.这表明PA∥EG.
而EG![]() 平面EDB且PA
平面EDB且PA![]() 平面EDB,
平面EDB,
∴PA∥平面EDB.
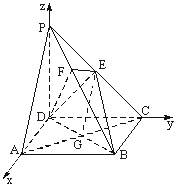
(Ⅱ)证明:依题意得B(a,a,0),![]() =(a,a,-a).
=(a,a,-a).
又![]() =(0,
=(0,![]() ,
, ![]() ),
),
故![]() ·
·![]() =0+
=0+![]() -
-![]() =0.
=0.
∴PB⊥DE.
由已知EF⊥PB,且EF∩DE=E,所以PB⊥平面EFD.
(Ⅲ)解:设点F的坐标为(x0,y0,z0),![]() =λ
=λ![]() ,则
,则
(x0,y0,z0-a)=λ(a,a,-a).
从而x0=λa,y0=λa,z0=(1-λ)a.
所以![]() =(-x0,
=(-x0,![]() -y0,
-y0,![]() -z0)=[-λa,(
-z0)=[-λa,(![]() -λ)a,(λ-
-λ)a,(λ-![]() )a].
)a].
由条件EF⊥PB知![]() ·
·![]() =0,即
=0,即
-λa2+(![]() -λ)a2-(λ-
-λ)a2-(λ-![]() )a2=0,
)a2=0,
解得λ=![]() .
.
∴点F的坐标为(![]() ,
,![]() ,
,![]() ),且
),且
![]() =(-
=(-![]() ,
,![]() ,-
,-![]() ),
),![]() =(-
=(-![]() ,-
,-![]() ,-
,-![]() ).
).
∴![]() ·
·![]() =-
=-![]() -
-![]() +
+![]() =0,
=0,
即PB⊥FD,故∠EFD是二面角C-PB-D的平面角.
∵![]() ·
·![]() =
=![]() -
-![]() +
+![]() =
=![]() ,且
,且
|![]() |=
|=![]() =
=![]() a,
a,
|![]() |=
|=![]() =
=![]() ,
,
∴cosEFD=![]() =
=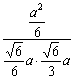 =
=![]() .
.
∴∠EFD=![]() .
.
所以,二面角C-PB-D的大小为![]() .
.


科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,PB与平面ABC成60°的角,底面ABCD是直角梯形,∠ABC=∠BAD=90°,AB=BC=
如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,PB与平面ABC成60°的角,底面ABCD是直角梯形,∠ABC=∠BAD=90°,AB=BC=| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2010•广东模拟)如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA垂直于底面ABCD,PA=AD=AB=2BC=2,M,N分别为PC,PB的中点.
(2010•广东模拟)如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA垂直于底面ABCD,PA=AD=AB=2BC=2,M,N分别为PC,PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,侧棱PA⊥底面ABCD,若AB=BC=
(2012•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,侧棱PA⊥底面ABCD,若AB=BC=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
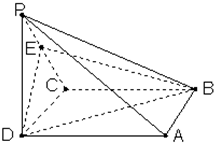 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,PD=DC,E是PC的中点.查看答案和解析>>
科目:高中数学 来源:浙江省瑞安中学2011-2012学年高二上学期期中考试数学理科试题 题型:047
如图,在四棱锥PA-ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面积ABCD,且![]() ,若E、F分别为PC、BD的中点.
,若E、F分别为PC、BD的中点.
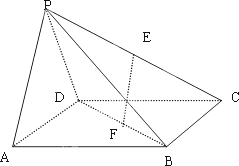
(Ⅰ)求证:EF∥平面PAD;
(Ⅱ)求证:PA⊥平面PDC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com