
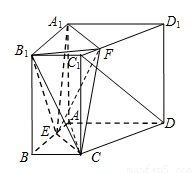
(本小题满分14分)如图,在四棱柱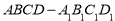 中,
中,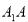
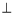 底面
底面 ,
,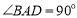 ,
,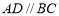 ,且
,且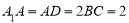 ,
, . 点E在棱AB上,平面
. 点E在棱AB上,平面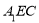 与棱
与棱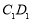 相交于点F.
相交于点F.
(Ⅰ)求证: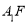 ∥平面
∥平面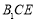 ;
;
(Ⅱ)求证: 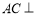 平面
平面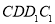 ;
;
(Ⅲ)写出三棱锥 体积的取值范围. (结论不要求证明)
体积的取值范围. (结论不要求证明)
(Ⅰ)详见解析; (Ⅱ)详见解析;(Ⅲ)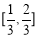 .
.
【解析】
试题分析:(Ⅰ)因为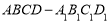 是棱柱,所以平面
是棱柱,所以平面 平面
平面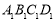 .由面面平行的性质定理,可得
.由面面平行的性质定理,可得 ∥
∥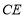 ,再根据线面平行的判定定理即可证明结论;(Ⅱ)在四边形ABCD中,因为
,再根据线面平行的判定定理即可证明结论;(Ⅱ)在四边形ABCD中,因为 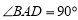 ,
, ,且
,且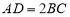 ,
,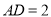 ,
,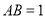 ,利用勾股定理可得,
,利用勾股定理可得, 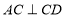 ,又
,又 .又
.又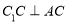 ,根据面面垂直的判定定理即可证明结果;(Ⅲ)由题意可知,三棱锥
,根据面面垂直的判定定理即可证明结果;(Ⅲ)由题意可知,三棱锥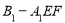 的体积的取值范围是
的体积的取值范围是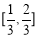 .
.
试题解析:(Ⅰ)证明:因为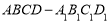 是棱柱,
是棱柱,
所以平面 平面
平面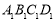 .
.
又因为平面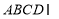 平面
平面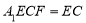 ,
,
平面 平面
平面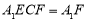 ,
,
所以  ∥
∥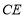 . 3分
. 3分
又 
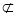 平面
平面 ,
,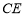
 平面
平面 ,
,
所以 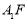 ∥平面
∥平面 . 6分
. 6分
(Ⅱ)证明:在四边形ABCD中,
因为 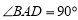 ,
, ,且
,且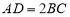 ,
,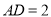 ,
,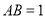 ,
,
所以 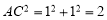 ,
,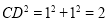 .
.
所以  ,
,
所以 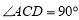 ,即
,即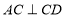 . 7分
. 7分
因为 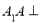 平面
平面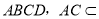 平面
平面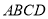 ,
,
所以  .
.
因为在四棱柱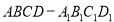 中,
中, ,
,
所以 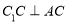 . 9分
. 9分
又因为 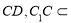 平面
平面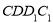 ,
, ,
,
所以 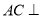 平面
平面 . 11分
. 11分
(Ⅲ)【解析】
三棱锥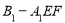 的体积的取值范围是
的体积的取值范围是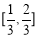 . 14分.
. 14分.
考点:1.线面平行的判定定理和性质定理;2.线面垂直的判定定理;3.锥体的体积公式.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中数学 来源:2014-2015学年江苏省连云港、徐州、淮安、宿迁四市高三一模考试理科数学试卷(解析版) 题型:解答题
(本小题满分10分)某校开设8门校本课程,其中4门课程为人文科学,4门为自然科学,学校要求学生在高中三年内从中选修3门课程,假设学生选修每门课程的机会均等.
(1)求某同学至少选修1门自然科学课程的概率;
(2)已知某同学所选修的3门课程中有1门人文科学,2门自然科学,若该同学通过人文科学课程的概率都是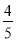 ,自然科学课程的概率都是
,自然科学课程的概率都是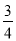 ,且各门课程通过与否相互独立.用
,且各门课程通过与否相互独立.用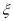 表示该同学所选的3门课程通过的门数,求随机变量
表示该同学所选的3门课程通过的门数,求随机变量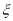 的概率分布列和数学期望。
的概率分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省惠州市高三第三次调研文科数学试卷(解析版) 题型:选择题
已知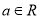 ,则“
,则“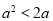 ”是“
”是“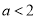 ”成立的( )
”成立的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省惠州市高三第三次调研理科数学试卷(解析版) 题型:填空题
某校有4000名学生,各年级男、女生人数如右表,已知在全校学生中随机抽取一名奥运火炬手,抽到高一男生的概率是0.2.现用分层抽样的方法在全校抽取100名奥运志愿者,则在高二抽取的学生人数为______.
高一 | 高二 | 高三 | |
女生 | 600 | y | 650 |
男生 | x | z | 750 |
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省惠州市高三第三次调研理科数学试卷(解析版) 题型:选择题
下列函数中,既是偶函数又在区间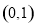 上单调递减的函数为( ).
上单调递减的函数为( ).
A.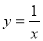 B.
B. C.
C.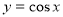 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市西城区高三上学期期末考试文科数学试卷(解析版) 题型:填空题
设 为双曲线C:
为双曲线C: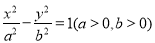 的左、右焦点,且直线
的左、右焦点,且直线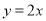 为双曲线C的一条渐近线,点P为C上一点,如果
为双曲线C的一条渐近线,点P为C上一点,如果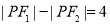 ,那么双曲线C的方程为____;离心率为_____.
,那么双曲线C的方程为____;离心率为_____.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市西城区高三上学期期末考试文科数学试卷(解析版) 题型:选择题
设函数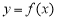 的定义域为
的定义域为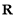 ,则“
,则“ ”是“函数
”是“函数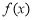 为奇函数”的( )
为奇函数”的( )
(A)充分而不必要条件
(B)必要而不充分条件
(C)充分必要条件
(D)既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市西城区高三上学期期末考试理科数学试卷(解析版) 题型:填空题
设D为不等式组 表示的平面区域,点
表示的平面区域,点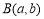 为坐标平面
为坐标平面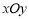 内一点,若对于区域D内的任一点
内一点,若对于区域D内的任一点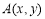 ,都有
,都有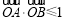 成立,则
成立,则 的最大值等于( )
的最大值等于( )
(A)2 (B)1 (C)0 (D)3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com