
分析 由题意可得f(x)在[1,+∞)上单调递增,f(1)=-3,f(2)=1,由此结合f(x)的图象可得$\left\{\begin{array}{l}{1-x<1}\\{{1≤2x}^{2}<2}\end{array}\right.$,或$\left\{\begin{array}{l}{1-x≥1}\\{1-x<{2x}^{2}}\end{array}\right.$,由此求得x的取值范围.
解答 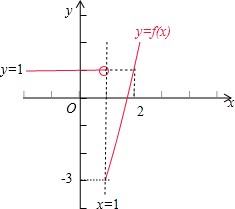 解:∵函数f(x)=$\left\{\begin{array}{l}{x^3}-3x-1\\ 1\end{array}\right.\begin{array}{l}{(x≥1)}\\{(x<1)}\end{array}$,
解:∵函数f(x)=$\left\{\begin{array}{l}{x^3}-3x-1\\ 1\end{array}\right.\begin{array}{l}{(x≥1)}\\{(x<1)}\end{array}$,
故当x≥1时,f′(x)=3x2-3≥0,
故f(x)在[1,+∞)上单调递增,f(1)=-3,f(2)=1.
故函数f(x)的图象如图所示:
则由不等式f(2x2)<f(1-x),
可得$\left\{\begin{array}{l}{1-x<1}\\{{1≤2x}^{2}<2}\end{array}\right.$,或$\left\{\begin{array}{l}{1-x≥1}\\{1-x<{2x}^{2}}\end{array}\right.$.
求得$\frac{\sqrt{2}}{2}$≤x<1 或x<-1,
故要求的x的取值范围为{x|$\frac{\sqrt{2}}{2}$≤x<1 或x<-1}.
点评 本题主要考查分段函数的应用,函数的单调性的应用,体现了转化、数形结合的数学思想,属于中档题.


科目:高中数学 来源: 题型:解答题
| 青年人 | 中年人 | 合计 | |
| 经常使用微信 | |||
| 不经常使用微信 | |||
| 合计 |
| P(K2≥k) | 0.010 | 0.001 |
| k | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x+2y-5=0 | B. | 2x-3y-5=0 | C. | 3x+2y+5=0 | D. | 3x-2y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
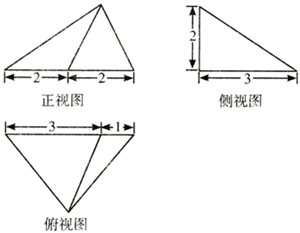
| A. | 12m3 | B. | $\frac{8}{3}{m^3}$ | C. | 4m3 | D. | 8m3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com