
分析 逐个验证各式是否符合三个条件即可得出答案.
解答 解:对于①,∵λ$\overrightarrow{X}$=(λx1,λx2),则||$λ\overrightarrow{X}$||=$\sqrt{{λ}^{2}{{x}_{1}}^{2}}$+2λ2x22,而|λ|||$\overrightarrow{X}$||=|λ|$\sqrt{{{x}_{1}}^{2}}$+|λ|x22,
∴||λ$\overrightarrow{X}$||≠|λ|•||$\overrightarrow{X}$||,不符合条件(2);
对于②,令||$\overrightarrow{X}$||=0得2x12-x22=0,故当x2=±$\sqrt{2}$x1时,||$\overrightarrow{X}$||=0,不符合条件(1);
对于③,当$\overrightarrow{X}$=(0,0)时,||$\overrightarrow{X}$||=$\sqrt{2}$≠0,不符合条件(1);
对于④,∵|||$\overrightarrow{X}$||=$\sqrt{{{x}_{1}}^{2}+{{x}_{2}}^{2}}$≥0,当且仅当x1=x2=0时取等号,故符合条件(1),
||λ$\overrightarrow{X}$||=$\sqrt{{λ}^{2}{{x}_{1}}^{2}+{λ}^{2}{{x}_{2}}^{2}}$=|λ|$\sqrt{{{x}_{1}}^{2}+{{x}_{2}}^{2}}$,故符合条件(2),
设$\overrightarrow{OA}=\overrightarrow{X}$,$\overrightarrow{OB}$=$\overrightarrow{Y}$=(x3,x4),$\overrightarrow{OC}=\overrightarrow{X}+\overrightarrow{Y}$,则||$\overrightarrow{X}$||=|OA|,||$\overrightarrow{Y}$||=|OB|,|$\overrightarrow{X}+\overrightarrow{Y}$|=|OC|,
在平行四边形OACB中,∵|AC|=|OB|,|OA|+|AC|>|OC|,
∴||$\overrightarrow{X}$||+||$\overrightarrow{Y}$||≥||$\overrightarrow{X}$+$\overrightarrow{Y}$||,故符合条件(3).
故答案为④.
点评 本题考查了平面向量的几何意义,坐标运算,属于中档题.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:填空题
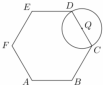 如图,在边长为2的正六边形ABCDEF中,动圆⊙Q的半径为1,圆心在线段CD(含端点)上运动,P为⊙Q上及内部的动点,设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AF}$(m,n∈R),则m+n的取值范围是[2,5].
如图,在边长为2的正六边形ABCDEF中,动圆⊙Q的半径为1,圆心在线段CD(含端点)上运动,P为⊙Q上及内部的动点,设向量$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AF}$(m,n∈R),则m+n的取值范围是[2,5].查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com