
| A. | (1,2) | B. | (2,+∞) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,+∞) |
分析 设其中一条渐近线与x轴的夹角为θ,由已知条件得tanθ<1,渐近线的方程为y=$\frac{b}{a}$x,从而$\frac{b}{a}$<1由此能求出该双曲线的离心率e的取值范围.
解答 解:如图,由△ABC为等腰直角三角形,所以∠BAx=45°,
设其中一条渐近线与x轴的夹角为θ,则θ<45°,即tanθ<1,
又上述渐近线的方程为y=$\frac{b}{a}$x,
则$\frac{b}{a}$<1,又e=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$,
∴1<e<$\sqrt{2}$,
双曲线的离心率e的取值范围(1,$\sqrt{2}$),
故选C.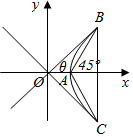
点评 本题考查双曲线的离心率的取值范围的求法,是中档题,解题时要认真审题,注意双曲线的性质的合理运用,属于中档题.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-2,2] | C. | {-1,0,1} | D. | {-2,-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
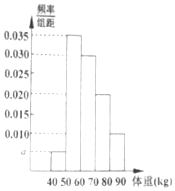 从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图),由直方图可知( )
从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图),由直方图可知( )| A. | 估计体重的众数为50或60 | |
| B. | a=0.03 | |
| C. | 学生体重在[50,60)有35人 | |
| D. | 从这100名男生中随机抽取一人,体重在[60,80)的概率为$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $x=\frac{π}{12}$ | B. | $x=-\frac{π}{3}$ | C. | $x=-\frac{π}{6}$ | D. | $x=\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
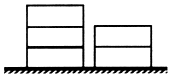 如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是( )
如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是( )| A. | 6 | B. | 10 | C. | 12 | D. | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com