
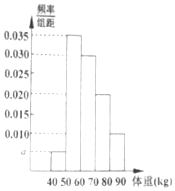
 从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图),由直方图可知( )
从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图),由直方图可知( )| A. | 估计体重的众数为50或60 | |
| B. | a=0.03 | |
| C. | 学生体重在[50,60)有35人 | |
| D. | 从这100名男生中随机抽取一人,体重在[60,80)的概率为$\frac{1}{3}$ |
分析 根据频率分布直方图,利用最高的小矩形对应的底边中点估计众数;
根据频率和为1,计算a的值;
计算体重在[50,60)内的频率和频数;
计算体重在[60,80)内的频率,用频率估计概率即可.
解答 解:根据频率分布直方图知,最高的小矩形对应的底边中点为$\frac{50+60}{2}$=55,∴估计众数为55,A错误;
根据频率和为1,计算(a+0.035+0.030+0.020+0.010)×10=1,解得a=0.005,B错误;
体重在[50,60)内的频率是0.35,估计体重在[50,60)有100×0.35=35人,C正确;
体重在[60,80)内的频率为0.3+0.2=0.5,用频率估计概率,
知这100名男生中随机抽取一人,体重在[60,80)的概率为$\frac{1}{2}$,D错误.
故选:C.
点评 本题考查了频率分布直方图,频率、频数与众数的计算问题.


科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 33 | C. | 35 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,+∞) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
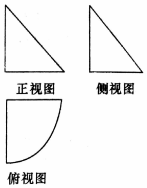 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为2的等腰直角三角形,俯视图是圆心角为$\frac{π}{2}$的扇形,则该几何体的表面积为( )
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为2的等腰直角三角形,俯视图是圆心角为$\frac{π}{2}$的扇形,则该几何体的表面积为( )| A. | 2 | B. | π+4 | C. | $\sqrt{2}π+4$ | D. | $({\sqrt{2}+1})π+4$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com