
 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD分析 (1)分别取EC,FC的中点G,H,连接GD,BH,HG,则四边形BHGD所确定的平面为平面α;
(2)取EF的中点N,连接AC交BD于点O,连接ON,由四边形BDEF为矩形,O,N分别为BD,EF的中点,可得ON∥ED.由面面垂直的性质可得ED⊥平面ABCD,进一步得到ON⊥平面ABCD.再由ABCD为菱形,可得AC⊥BD.以O为原点,OB,OC,ON所在直线分别为x轴,y轴,z轴,如图建立空间直角坐标系.然后利用空间向量求FB与平面α所成角的正弦值.
解答 解:(1)如图所示,分别取EC,FC的中点G,H,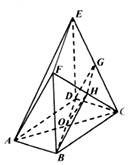
连接GD,BH,HG,四边形BHGD所确定的平面为平面α.
(2)取EF的中点N,连接AC交BD于点O,连接ON,
∵四边形BDEF为矩形,O,N分别为BD,EF的中点,
∴ON∥ED.
∵平面BDEF⊥平面ABCD,
∴ED⊥平面ABCD,则ON⊥平面ABCD.
∵ABCD为菱形,即AC⊥BD.
以O为原点,OB,OC,ON所在直线分别为x轴,y轴,z轴,如图建立空间直角坐标系.
∵平面α∥平面AEF,∴BF与平面α所成的角可以转化为BF与平面AEF所成的角,则平面AEF与平面ABCD所成角为45°.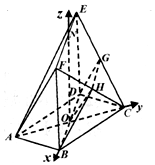
设FB=a,则A(0,$-\sqrt{3}$,0),E(-1,0,a),F(1,0,a),$\overrightarrow{AE}=(-1,\sqrt{3},a)$,$\overrightarrow{AF}=(1,\sqrt{3},a)$,B(1,0,0),
设平面AEF的法向量为$\overrightarrow{n}=(x,y,z)$,
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AE}=-x+\sqrt{3}y+az=0}\\{\overrightarrow{n}•\overrightarrow{AF}=x+\sqrt{3}y+az=0}\end{array}\right.$,令z=1,得$\overrightarrow{n}=(0,-\frac{a}{\sqrt{3}},1)$.
易看出$\overrightarrow{m}=(0,0,1)$是平面ABCD的一个法向量,依题得$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}=\frac{\sqrt{2}}{2}$,即$\frac{1}{\sqrt{\frac{{a}^{2}}{3}+1}}=\frac{\sqrt{2}}{2}$,解得a=$\sqrt{3}$.
∴$\overrightarrow{n}=(0,-1,1)$,又$\overrightarrow{BF}=(0,0,\sqrt{3})$,∴cos<$\overrightarrow{n},\overrightarrow{BF}$>=$\frac{\sqrt{2}}{2}$,
即FB与平面α所成角的正弦值为$\frac{\sqrt{2}}{2}$.
点评 本题考查直线与平面平行的判定,考查线面角的求法,训练了利用空间向量求线面角,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
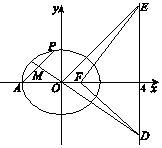 如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{1}{2}$,F为椭圆C的右焦点.A(-a,0),|AF|=3.
如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{1}{2}$,F为椭圆C的右焦点.A(-a,0),|AF|=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
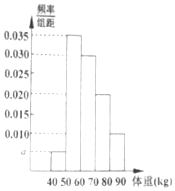 从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图),由直方图可知( )
从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图),由直方图可知( )| A. | 估计体重的众数为50或60 | |
| B. | a=0.03 | |
| C. | 学生体重在[50,60)有35人 | |
| D. | 从这100名男生中随机抽取一人,体重在[60,80)的概率为$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{1,e+\frac{1}{e}}]$ | B. | $[{1,e-\frac{1}{e}}]$ | C. | $[{e-\frac{1}{e},e+\frac{1}{e}}]$ | D. | $[{e-\frac{1}{e},e}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
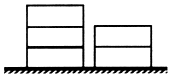 如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是( )
如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是( )| A. | 6 | B. | 10 | C. | 12 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x+3)2+(y-1)2=1 | B. | (x-3)2+(y+1)2=1 | C. | (x+3)2+(y+1)2=1 | D. | (x-3)2+(y-1)2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
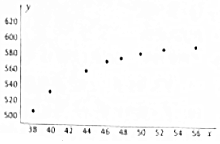 在一项调查中有两个变量x(单位:千元)和y(单位:t),如图是由这两个变量近8年来的取值数据得到的散点图,那么适宜作为y关于x的回归方程类型的是( )
在一项调查中有两个变量x(单位:千元)和y(单位:t),如图是由这两个变量近8年来的取值数据得到的散点图,那么适宜作为y关于x的回归方程类型的是( )| A. | y=a+bx | B. | y=c+d$\sqrt{x}$ | C. | y=m+nx2 | D. | y=p+qex(q>0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com