练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
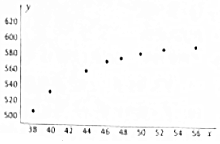
    19．在一项调查中有两个变量x（单位：千元）和y（单位：t），如图是由这两个变量近8年来的取值数据得到的散点图，那么适宜作为y关于x的回归方程类型的是（　　）
    A．y=a+bxB．y=c+d$\sqrt{x}$C．y=m+nx2D．y=p+qex（q＞0）

    分析 由散点图可得，图象是抛物线形状，则适宜作为y关于x的回归方程类型的是y=c+d$\sqrt{x}$．

    解答 解：由散点图可得，图象是抛物线形状，则适宜作为y关于x的回归方程类型的是y=c+d$\sqrt{x}$，
    故选B．

    点评 本题考查散点图，考查数形结合的数学思想，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    9．如图，在多面体ABCDEF中，底面ABCD是边长为2的菱形，∠BAD=60°，四边形BDEF是矩形，平面BDEF⊥平面ABCD
    （1）在图中画出过点B，D的平面α，使得α∥平面AEF（必须说明画法，不需证明）；
    （2）若二面角α-BD-C是45°，求FB与平面α所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{2}{3}$，F1，F2分别是它的左、右焦点，且存在直线l，使F1，F2关于l的对称点恰好为圆C：x2+y2-4mx-2my+5m2-4=0（m∈R，m≠0）的一条直径的两个端点．
    （1）求椭圆E的方程；
    （2）设直线l与抛物线y2=2px（p＞0）相交于A，B两点，射线F1A，F1B与椭圆E分别相交于点M，N，试探究：是否存在数集D，当且仅当p∈D时，总存在m，使点F1在以线段MN为直径的圆内？若存在，求出数集D；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．复数z=（1+i）+（-2+2i）在复平面内对应的点位于第二象限．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．若数列{An}对任意的n∈N*，都有${A_{n+1}}={A_n}^k$（k≠0），且An≠0，则称数列{An}为“k级创新数列”．
    （1）已知数列{an}满足${a_{n+1}}=2{a_n}^2+2{a_n}$且${a_1}=\frac{1}{2}$，试判断数列{2an+1}是否为“2级创新数列”，并说明理由；
    （2）已知正数数列{bn}为“k级创新数列”且k≠1，若b1=10，求数列{bn}的前n项积Tn；
    （3）设α，β是方程x2-x-1=0的两个实根（α＞β），令$k=\frac{β}{α}$，在（2）的条件下，记数列{cn}的通项${c_n}={β^{n-1}}•{log_{b_n}}{T_n}$，求证：cn+2=cn+1+cn，n∈N*．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知正三棱柱ABC-A1B1C1的顶点A1，B1，C1在同一球面上，且平面ABC经过球心，若此球的表面积为4π，则该三棱柱的侧面积的最大值为（　　）
    A．$\frac{\sqrt{3}}{2}$B．$\sqrt{3}$C．$\frac{3\sqrt{3}}{2}$D．3$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．f（x）=sin（ωx+φ）（ω＜0）向右平移$\frac{π}{12}$个单位之后图象与g（x）=cos2x的图象重合，则φ=（　　）
    A．$\frac{5}{12}$πB．$\frac{π}{3}$C．$\frac{5}{12}$π+2kπ（k∈Z）D．$\frac{π}{3}$+2kπ（k∈Z）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．在△ABC中，若a=18，b=24，A=30°，则此三角形解的个数为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．如图，G是△ABC的重心，D为BC的中点，$\overrightarrow{AB}+\overrightarrow{AC}$=λ$\overrightarrow{GD}$，则λ的值为（　　）
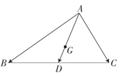
    A．3B．4C．6D．12

    查看答案和解析>>

    同步练习册答案