
分析 (1)数列{2an+1}是“2级创新数列”,下面给出证明:${a_{n+1}}=2{a_n}^2+2{a_n}$,可得an+1+1=$4{a}_{n}^{2}+4{a}_{n}$+1=$(2{a}_{n}+1)^{2}$≠0,即可证明.
(2)正数数列{bn}为“k级创新数列”且k≠1,${b}_{n+1}={b}_{n}^{k}$.bn=${b}_{n-1}^{k}$=$({b}_{n-2}^{k})^{k}$=…=${b}_{1}^{{k}^{n-1}}$=$1{0}^{{k}^{n-1}}$.又b1=10,利用指数的运算性质可得数列{bn}的前n项积Tn=$1{0}^{\frac{{k}^{n}-1}{k-1}}$.
(3)α,β是方程x2-x-1=0的两个实根(α>β),可得β2-β-1=0,α2-α-1=0.在(2)的条件下,记数列{cn}的通项${c_n}={β^{n-1}}•{log_{b_n}}{T_n}$=βn-1×$\frac{\frac{{k}^{n}-1}{k-1}}{{k}^{n-1}}$=$\frac{{β}^{n}-{α}^{n}}{β-α}$.
解答 (1)解:数列{2an+1}是“2级创新数列”,下面给出证明:
∵${a_{n+1}}=2{a_n}^2+2{a_n}$,∴2an+1+1=$4{a}_{n}^{2}+4{a}_{n}$+1=$(2{a}_{n}+1)^{2}$≠0,
∴数列{2an+1}是“2级创新数列”.
(2)解:∵正数数列{bn}为“k级创新数列”且k≠1,∴${b}_{n+1}={b}_{n}^{k}$.
∴bn=${b}_{n-1}^{k}$=$({b}_{n-2}^{k})^{k}$=${b}_{n-2}^{{k}^{2}}$=…=${b}_{1}^{{k}^{n-1}}$=$1{0}^{{k}^{n-1}}$.
又b1=10,∴数列{bn}的前n项积Tn=bnbn-1•…•b1=$1{0}^{{k}^{n-1}+{k}^{n-2}+…+k+1}$=$1{0}^{\frac{{k}^{n}-1}{k-1}}$.
(3)证明:α,β是方程x2-x-1=0的两个实根(α>β),
∴β2-β-1=0,α2-α-1=0.
在(2)的条件下,记数列{cn}的通项${c_n}={β^{n-1}}•{log_{b_n}}{T_n}$=βn-1×$\frac{\frac{{k}^{n}-1}{k-1}}{{k}^{n-1}}$
=βn-1×$\frac{(\frac{β}{α})^{n}-1}{(\frac{β}{α})^{n-1}(\frac{β}{α}-1)}$=$\frac{{β}^{n}-{α}^{n}}{β-α}$.
∴cn+2=$\frac{{β}^{n+2}-{α}^{n+2}}{β-α}$.cn+1+cn=$\frac{{β}^{n+1}-{α}^{n+1}}{β-α}$+$\frac{{β}^{n}-{α}^{n}}{β-α}$.
∴cn+2-(cn+1+cn)=$\frac{{β}^{n}({β}^{2}-β-1)+{α}^{n}({α}^{2}-α-1)}{β-α}$=0.
∴cn+2=cn+1+cn.
点评 本题考查了数列递推关系、指数的运算性质、一元二次风吹草动根与系数的关系、作差法,考查了推理能力、计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
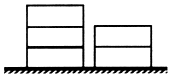 如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是( )
如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是( )| A. | 6 | B. | 10 | C. | 12 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2017 | B. | 2016 | C. | 2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
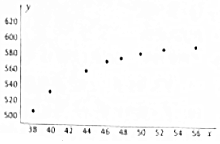 在一项调查中有两个变量x(单位:千元)和y(单位:t),如图是由这两个变量近8年来的取值数据得到的散点图,那么适宜作为y关于x的回归方程类型的是( )
在一项调查中有两个变量x(单位:千元)和y(单位:t),如图是由这两个变量近8年来的取值数据得到的散点图,那么适宜作为y关于x的回归方程类型的是( )| A. | y=a+bx | B. | y=c+d$\sqrt{x}$ | C. | y=m+nx2 | D. | y=p+qex(q>0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com