练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．在△ABC中，若a=18，b=24，A=30°，则此三角形解的个数为2．

    分析 根据余弦定理，建立a2关于b、c和cosA的式子，得到关于边c的一元二次方程，解之得c有2解，由此可得此三角形有两解，得到本题的答案．

    解答 解：由△ABC中，a=18，b=24，A=30°，
    由余弦定理a2=b2+c2-2bccosA，得182=242+c2-2×24ccos30°，
    化简整理，得c2-24$\sqrt{3}$c+252=0，
    由于△=（24$\sqrt{3}$）2-4×252=720＞0，
    可得c有2解，可得此三角形解的个数有2个．
    故答案为：2．

    点评 本题给出三角形两边及一边对夹角的大小，求三角形的解的个数，着重考查了利用正弦定理和余弦定理解三角形的知识，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=lnx，g（x）=$\frac{1}{2}$x2-bx（b为常数）．
    （1）函数f（x）的图象在点（1，f（1））处的切线与函数g（x）的图象相切，求实数b的值；
    （2）若函数h（x）=f（x）+g（x）在定义域上存在单调减区间，求实数b的取值范围；
    （3）若b≥2，?x1，x2∈[1，2]，且x1≠x2，都有|f（x1）-f（x2）|＞|g（x1）-g（x2）|成立，求实数b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

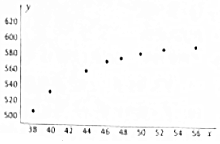    19．在一项调查中有两个变量x（单位：千元）和y（单位：t），如图是由这两个变量近8年来的取值数据得到的散点图，那么适宜作为y关于x的回归方程类型的是（　　）
    A．y=a+bxB．y=c+d$\sqrt{x}$C．y=m+nx2D．y=p+qex（q＞0）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知集合A={y|y=$\frac{4{-e}^{x}}{2}$，x∈R}，B={x|y=lg（1-2x）}
    （1）求出集合A，集合B；
    （2）求（∁UB）∩A．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．证明：a2+b2+c2=ab+bc+ca的充要条件是△ABC为等边三角形．这里a，b，c是△ABC的三条边．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知f（x）=x2-（m+$\frac{1}{m}$）x+1
    （1）当m=2时，解不等式f（x）≤0
    （2）若m＞0，解关于x的不等式f（x）≥0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知向量$\overrightarrow a$=（{cosx，-$\sqrt{3}$cosx），$\overrightarrow b$=（cosx，sinx），函数f（x）=$\overrightarrow a$•$\overrightarrow b$+1．
    （Ⅰ）求函数f（x）的单调递增区间；
    （Ⅱ）若f（θ）=$\frac{5}{6}$，$θ∈（\frac{π}{3}，\frac{2π}{3}），求sin2θ$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

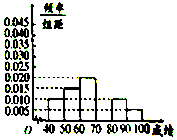    17．如图是从成都某中学参加高三体育考试的学生中抽出的40名学生体育成绩（均为整数）的频率分布直方图，该直方图恰好缺少了成绩在区间[70，80）内的图形，根据图形的信息，回答下列问题：
    （1）求成绩在区间[70，80）内的频率，并补全这个频率分布直方图，并估计这次考试的及格率（60分及以上为及格）；
    （2）从成绩在[80，100]内的学生中选出三人，记在90分以上（含90分）的人数为X，求X的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知函数f（x）是R上的偶函数，且满足f（x+2）=-f（x），当x∈[0，1]时，f（x）=2-x，则f（2016）+f（-2017）的值为3．

    查看答案和解析>>

    同步练习册答案