
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | 3$\sqrt{3}$ |
分析 求出此球半径R=1,设三棱柱正三棱柱ABC-A1B1C1的顶点A1,B1,C1所在球面的小圆的半径为r,球心到顶点A1,B1,C1所在球面的小圆的距离为d,由勾股定理得r2+d2=R2=1,由此利用均值定理能求出该三棱柱的侧面积的最大值.
解答 解:∵正三棱柱ABC-A1B1C1的顶点A1,B1,C1在同一球面上,
且平面ABC经过球心,此球的表面积为4π,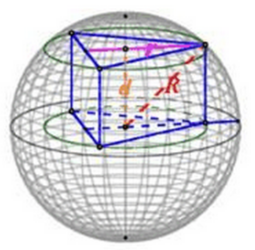
∴此球半径R=1,
如图,设三棱柱正三棱柱ABC-A1B1C1的顶点
A1,B1,C1所在球面的小圆的半径为r,
球心到顶点A1,B1,C1所在球面的小圆的距离为d,
则r2+d2=R2=1,
∴该三棱柱的侧面积:
S=3×$\sqrt{3}×r×d$≤3$\sqrt{3}$×$\frac{{r}^{2}+{d}^{2}}{2}$=3$\sqrt{3}×\frac{1}{2}$=$\frac{3\sqrt{3}}{2}$.
∴该三棱柱的侧面积的最大值为$\frac{3\sqrt{3}}{2}$.
故选:C.
点评 本题考查三棱柱、球、勾股定理等基础知识,考查抽象概括能力、数据处理能力、运算求解能力,考查应用意识、创新意识,考查化归与转化思想、分类与整合思想、数形结合思想,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (x+3)2+(y-1)2=1 | B. | (x-3)2+(y+1)2=1 | C. | (x+3)2+(y+1)2=1 | D. | (x-3)2+(y-1)2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 86 | B. | 88 | C. | 90 | D. | 92 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
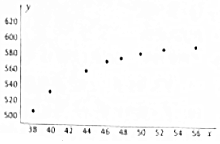 在一项调查中有两个变量x(单位:千元)和y(单位:t),如图是由这两个变量近8年来的取值数据得到的散点图,那么适宜作为y关于x的回归方程类型的是( )
在一项调查中有两个变量x(单位:千元)和y(单位:t),如图是由这两个变量近8年来的取值数据得到的散点图,那么适宜作为y关于x的回归方程类型的是( )| A. | y=a+bx | B. | y=c+d$\sqrt{x}$ | C. | y=m+nx2 | D. | y=p+qex(q>0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2016}$ | B. | $\frac{1}{2017}$ | C. | $\frac{1}{2018}$ | D. | $\frac{1}{2019}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com