练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．如图，G是△ABC的重心，D为BC的中点，$\overrightarrow{AB}+\overrightarrow{AC}$=λ$\overrightarrow{GD}$，则λ的值为（　　）
    A．3B．4C．6D．12

    分析 根据向量加法的平行四边形法则，求和得到结果．

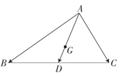
    解答 解：∵点G是△ABC的重心，D是AB的中点，
    $\overrightarrow{GD}$=$\frac{1}{3}$$\overrightarrow{AD}$=$\frac{1}{3}$（$\overrightarrow{AB}$+$\overrightarrow{BD}$）=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{BC}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{1}{6}$（$\overrightarrow{AC}$-$\overrightarrow{AB}$）=$\frac{1}{6}$$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AC}$=$\frac{1}{λ}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$），
    ∴λ=6，
    故选：C．

    点评 本题考查三角形的重心，考查三角形重心的性质，考查向量加法的平行四边形法则，考查向量的加减运算，是一个比较简单的综合题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

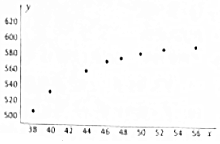    19．在一项调查中有两个变量x（单位：千元）和y（单位：t），如图是由这两个变量近8年来的取值数据得到的散点图，那么适宜作为y关于x的回归方程类型的是（　　）
    A．y=a+bxB．y=c+d$\sqrt{x}$C．y=m+nx2D．y=p+qex（q＞0）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知向量$\overrightarrow a$=（{cosx，-$\sqrt{3}$cosx），$\overrightarrow b$=（cosx，sinx），函数f（x）=$\overrightarrow a$•$\overrightarrow b$+1．
    （Ⅰ）求函数f（x）的单调递增区间；
    （Ⅱ）若f（θ）=$\frac{5}{6}$，$θ∈（\frac{π}{3}，\frac{2π}{3}），求sin2θ$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

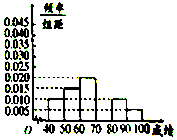    17．如图是从成都某中学参加高三体育考试的学生中抽出的40名学生体育成绩（均为整数）的频率分布直方图，该直方图恰好缺少了成绩在区间[70，80）内的图形，根据图形的信息，回答下列问题：
    （1）求成绩在区间[70，80）内的频率，并补全这个频率分布直方图，并估计这次考试的及格率（60分及以上为及格）；
    （2）从成绩在[80，100]内的学生中选出三人，记在90分以上（含90分）的人数为X，求X的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数F（x）与f（x）=lnx的图象关于直线y=x对称．
    （Ⅰ）不等式xf（x）≥ax-1对任意x∈（0，+∞）恒成立，求实数a的最大值；
    （Ⅱ）设f（x）F（x）=1在（1，+∞）内的实根为x0，m（x）=$\left\{\begin{array}{l}{xf（x），1＜x≤{x}_{0}}\\{\frac{x}{F（x）}，x＞{x}_{0}}\end{array}\right.$，若在区间（1，+∞）上存在m（x1）=m（x2）（x1＜x2），证明：$\frac{{x}_{1}+{x}_{2}}{2}$＞x0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．在△ABC中，已知a=2，b=2$\sqrt{3}$，B=120°，解此三角形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知函数f（x）=$\frac{{e}^{x+b}}{x}$过点（1，e）．
    （1）求y=f（x）的单调区间；
    （2）当x＞0时，求$\frac{f（x）}{x}$的最小值；
    （3）试判断方程f（x）-mx=0（m∈R且m为常数）的根的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知函数f（x）是R上的偶函数，且满足f（x+2）=-f（x），当x∈[0，1]时，f（x）=2-x，则f（2016）+f（-2017）的值为3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．观察（1）sin220°+cos250°+sin20°cos50°=$\frac{3}{4}$；（2）sin28°+cos238°+sin8°cos38°=$\frac{3}{4}$，两式的结构特点可提出一个猜想的等式为sin2α+cos2（α+30°）+sinαcos（α+30°）=$\frac{3}{4}$．

    查看答案和解析>>

    同步练习册答案