
分析 (1)求得圆心与半径,由c=2,根据离心率公式即可求得a和b的值,求得椭圆方程;
(2)求得直线l的方程,代入椭圆方程,利用韦达定理,及向量数量积的坐标运算$\overrightarrow{{F}_{1}A}$•$\overrightarrow{{F}_{1}B}$<0,代入即可求得求得.
解答 解:(1)将圆C的方程配方的:(x-2m)2+(y-m)2=4,则圆心C(2m,m),半径为2,
由椭圆的焦距为2c=d=4,c=2,
由e=$\frac{c}{a}$=$\frac{2}{3}$,则a=3,
b2=a2-c2=5,故椭圆的方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1$;
(2)由F1,F2关于l的对称点恰好是圆C的一条直径的两个端点,则直线l是线段OC的垂直平分线,
故l方程为y=-2x+$\frac{5m}{2}$,
$\left\{\begin{array}{l}{{y}^{2}=2px}\\{y=-2x+\frac{5m}{2}}\end{array}\right.$,整理得2y2+2py-5pm=0,
则△=(2p)2+4×2×5p>0,则p+10m>0,
设A(x1,y1),B(x1,y1),则y1+y2=-p,y1y1=-$\frac{5}{2}pm$,
由F1的坐标为(-2,0),则$\overrightarrow{{F}_{1}A}$=(x1+2,y1),$\overrightarrow{{F}_{1}B}$=(x2+2,y2),
由$\overrightarrow{{F}_{1}M}$与$\overrightarrow{{F}_{1}A}$同向,$\overrightarrow{{F}_{1}N}$与$\overrightarrow{{F}_{1}B}$同向,
则点F1在以线段MN为直径的圆内,则$\overrightarrow{{F}_{1}M}$•$\overrightarrow{{F}_{1}N}$<0,则$\overrightarrow{{F}_{1}A}$•$\overrightarrow{{F}_{1}B}$<0,
则(x1+2)(x2+2)+y1y2<0,即x1x2+2(x1+x2)+4+y1y1<0,则$\frac{25{m}^{2}}{4}$+10(2-p)m+4(p+4)<0,
当且仅当△=100(2-p)2-100(p+4)>0,即p>5,
总存在m使得②成立,
当p>5时,由韦达定理可知$\frac{25{m}^{2}}{4}$+10(2-p)m+4(p+4)=0的两个根为正数,
故使②成立的m>0,从而满足①,
故存在整数集D=(5,+∞),当且仅当p∈D时,总存在m,使点F1在线段MN为直径的圆内.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理及向量数量积的坐标运算,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
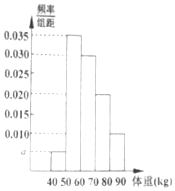 从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图),由直方图可知( )
从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图),由直方图可知( )| A. | 估计体重的众数为50或60 | |
| B. | a=0.03 | |
| C. | 学生体重在[50,60)有35人 | |
| D. | 从这100名男生中随机抽取一人,体重在[60,80)的概率为$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 86 | B. | 88 | C. | 90 | D. | 92 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2017 | B. | 2016 | C. | 2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
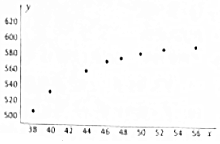 在一项调查中有两个变量x(单位:千元)和y(单位:t),如图是由这两个变量近8年来的取值数据得到的散点图,那么适宜作为y关于x的回归方程类型的是( )
在一项调查中有两个变量x(单位:千元)和y(单位:t),如图是由这两个变量近8年来的取值数据得到的散点图,那么适宜作为y关于x的回归方程类型的是( )| A. | y=a+bx | B. | y=c+d$\sqrt{x}$ | C. | y=m+nx2 | D. | y=p+qex(q>0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com