
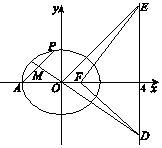
 如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{1}{2}$,F为椭圆C的右焦点.A(-a,0),|AF|=3.
如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{1}{2}$,F为椭圆C的右焦点.A(-a,0),|AF|=3.分析 (Ⅰ)由题意可知:a=2c,a+c=3,求得a与c的值,则b2=a2-c2,即可求得椭圆方程;
(Ⅱ)解法一:设AP的方程,代入椭圆方程,利用韦达定理及中点坐标公式求得M坐标,求得直线OM的方程,分别取得D和E点坐标,则EF⊥OM,DF⊥OE,在Rt△EHO和Rt△DGO中,∠ODF和∠OEF都与∠EOD互余,即可求得∠ODF=∠OEF;
方法二:分别表示出M,D和E点坐标,求得EF和OM的斜率,由kOM•kEF=-1,则EF⊥OM,讨论证明DF⊥OE在,则Rt△EHO和Rt△DGO中,∠ODF和∠OEF都与∠EOD互余,即可求得∠ODF=∠OEF.
解答 解:(Ⅰ)设椭圆C的半焦距为c.椭圆的离心率e=$\frac{c}{a}=\frac{1}{2}$,丨AF丨=a+c=3,
解得 a=2,c=1.
所以 b2=a2-c2=3,
所以椭圆C的方程是 $\frac{x^2}{4}+\frac{y^2}{3}=1$.[(4分)]
(Ⅱ)解法一:由(Ⅰ)得 A(-2,0).设AP的中点M(x0,y0),P(x1,y1).
设直线AP的方程为:y=k(x+2)(k≠0),
将其代入椭圆方程,整理得(4k2+3)x2+16k2x+16k2-12=0,[(6分)]
所以 $-2+{x_1}=\frac{{-16{k^2}}}{{4{k^2}+3}}$.[(7分)]
所以 ${x_0}=\frac{{-8{k^2}}}{{4{k^2}+3}}$,${y_0}=k({x_0}+2)=\frac{6k}{{4{k^2}+3}}$,
即 $M(\frac{{-8{k^2}}}{{4{k^2}+3}},\frac{6k}{{4{k^2}+3}})$.[(8分)]
所以直线OM的斜率是 $\frac{{\frac{6k}{{4{k^2}+3}}}}{{\frac{{-8{k^2}}}{{4{k^2}+3}}}}=-\frac{3}{4k}$,[(9分)]
所以直线OM的方程是 $y=-\frac{3}{4k}x$.令x=4,得$D(4,-\frac{3}{k})$.[(10分)]
直线OE的方程是 y=kx.令x=4,得E(4,4k).[(11分)]
由F(1,0),得直线EF的斜率是 $\frac{4k}{4-1}=\frac{4k}{3}$,所以EF⊥OM,记垂足为H;
因为直线DF的斜率是 $\frac{{-\frac{3}{k}}}{4-1}=-\frac{1}{k}$,所以DF⊥OE,记垂足为G.[(13分)]
在Rt△EHO和Rt△DGO中,∠ODF和∠OEF都与∠EOD互余,
所以∠ODF=∠OEF.[(14分)]
解法二:由(Ⅰ)得 A(-2,0).设P(x1,y1)(x1≠±2),其中$3x_1^2+4y_1^2-12=0$.
因为AP的中点为M,所以 $M(\frac{{{x_1}-2}}{2},\frac{y_1}{2})$.[(6分)]
所以直线OM的斜率是 ${k_{OM}}=\frac{y_1}{{{x_1}-2}}$,[(7分)]
所以直线OM的方程是 $y=\frac{y_1}{{{x_1}-2}}x$.令x=4,得$D(4,\frac{{4{y_1}}}{{{x_1}-2}})$.[(8分)]
直线OE的方程是 $y=\frac{y_1}{{{x_1}+2}}x$.令x=4,得$E(4,\frac{{4{y_1}}}{{{x_1}+2}})$.[(9分)]
由F(1,0),得直线EF的斜率是 ${k_{EF}}=\frac{{4{y_1}}}{{3({x_1}+2)}}$,[(10分)]
因为 ${k_{EF}}•{k_{OM}}=\frac{{4{y_1}}}{{3({x_1}+2)}}•\frac{y_1}{{{x_1}-2}}=\frac{4y_1^2}{3(x_1^2-4)}=-1$,
所以EF⊥OM,记垂足为H;[(12分)]
同理可得 ${k_{DF}}•{k_{OE}}=\frac{{4{y_1}}}{{3({x_1}-2)}}•\frac{y_1}{{{x_1}+2}}=\frac{4y_1^2}{3(x_1^2-4)}=-1$,
所以DF⊥OE,记垂足为G.[(13分)]
在Rt△EHO和Rt△DGO中,∠ODF和∠OEF都与∠EOD互余,
所以∠ODF=∠OEF.[(14分)]
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理,中点坐标公式,直线的斜率公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 33 | C. | 35 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | (-∞,1) | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com