
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:解答题
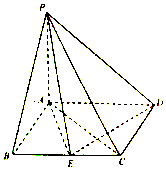 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥底面ABCD,AB⊥AC,AB=1,BC=2,PA=$\frac{\sqrt{2}}{2}$,E为BC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥底面ABCD,AB⊥AC,AB=1,BC=2,PA=$\frac{\sqrt{2}}{2}$,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 |
| 汽车越野赛届编号x | 1 | 2 | 3 | 4 | 5 |
| 外地游客人数y(单位:十万) | 0.6 | 0.8 | 0.9 | 1.2 | 1.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
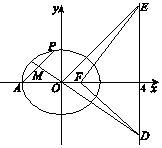 如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{1}{2}$,F为椭圆C的右焦点.A(-a,0),|AF|=3.
如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{1}{2}$,F为椭圆C的右焦点.A(-a,0),|AF|=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
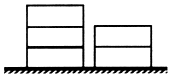 如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是( )
如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是( )| A. | 6 | B. | 10 | C. | 12 | D. | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com