
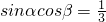 ,则sinβcosα的取值范围是________.
,则sinβcosα的取值范围是________.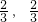 ]
] +sinβcosα,sin(α-β)=sinαcosβ-cosαsinβ=
+sinβcosα,sin(α-β)=sinαcosβ-cosαsinβ= -sinβcosα,sin(α+β) sin(α-β)∈[-1,1],知-1
-sinβcosα,sin(α+β) sin(α-β)∈[-1,1],知-1 +sinβcosα≤1,由此能导出
+sinβcosα≤1,由此能导出 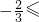 sinβcosα
sinβcosα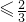 .
. +sinβcosα
+sinβcosα  -sinβcosα
-sinβcosα +sinβcosα≤1
+sinβcosα≤1 ≤sinβcosα
≤sinβcosα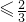 ,
, -sinβcosα≤1
-sinβcosα≤1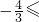 -sinβcosα
-sinβcosα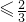 ,
,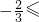 sinβcosα
sinβcosα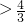 ,
,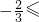 sinβcosα
sinβcosα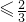 .
.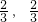 ].
].

 计算高手系列答案
计算高手系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com