考点:数列与函数的综合
专题:综合题,等差数列与等比数列
分析:(1)根据题中已知条件以及等差数列的基本性质,先求出bn的通项公式,然后证明为常数即可证明;
(2)先求出bn的通项公式,然后求出cn的表达式,可知数列cn随n增大而减小,故c1≤t,便可求出t的最小值;
(3)根据题意先求出dn的表达式,然后求出Sn的表达式,因为2014-1120=894=298×3,是3的倍数,所以存在自然数m,使Sm=2014.
解答:
解:(1)设等差数列的公差为d,则
由已知b
n=
()an,∵数列{a
n}是等差数列,
∴
=
()d(常数),
∴数列{b
n}是等比数列.
(2)∵a
n=n,∴b
n=
()n∴c
n=
(n+2)2•()n+2,
∴
=
<1,
∴数列{c
n}随n增大而减小,
∵c
n≤t对一切正整数n恒成立
∴c
1≤t,
∴t≥
,
∴最小的实数t为
;
(3))∵a
n=n,∴数列{d
n}中,从第一项a
1开始到a
k为止(含a
k项)的所有项的和是(1+2+…+k)+(3
1+3
2+…+3
k-1)=
+
,
当k=7时,其和是28+
=1120<2014,而当k=8时,其和是36+
=3315>2014,
又∵2014-1120=894=298×3,是3的倍数,
所以存在自然数m,使S
m=2014.
此时m=7+(1+3+3
2+…+3
5)+298=669.
点评:本题考查了等差数列和等比数列的基本性质以及函数的综合应用,考查了学生的计算能力和对数列的综合掌握,解题时注意整体思想和转化思想的运用,属于中档题.



 阅读快车系列答案
阅读快车系列答案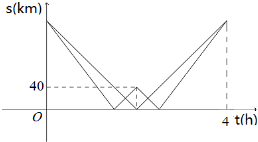 A,B两架直升机同时从机场出发,完成某项救灾物资空投任务.A机到达甲地完成任务后原路返回;B机路过甲地,前往乙地完成任务后原路返回.如图中折线分别表示A,B两架直升机离甲地的距离s与时间t之间的函数关系.假设执行任务过程中A,B均匀速直线飞行,则B机每小时比A机多飞行
A,B两架直升机同时从机场出发,完成某项救灾物资空投任务.A机到达甲地完成任务后原路返回;B机路过甲地,前往乙地完成任务后原路返回.如图中折线分别表示A,B两架直升机离甲地的距离s与时间t之间的函数关系.假设执行任务过程中A,B均匀速直线飞行,则B机每小时比A机多飞行

 如图,已知椭圆E:
如图,已知椭圆E: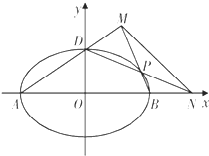 已知椭圆
已知椭圆