
(本小题12分)若点![]() ,在
,在![]() 中按均匀分布出现. (1)点
中按均匀分布出现. (1)点![]() 横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,则点
横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,则点![]() 落在上述区域内的概率?(2)试求方程
落在上述区域内的概率?(2)试求方程![]() 有两个实数根的概率.
有两个实数根的概率.
解:解析:(1)如图所示 ,点![]() 横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,试验的全部结果共有36种基本事件,且每个基本事件发生的可能性是相等的,符合古点概型的条件。 (2分)
横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,试验的全部结果共有36种基本事件,且每个基本事件发生的可能性是相等的,符合古点概型的条件。 (2分)
设A为“点![]() 落在满足条件的区域内”的事件,事件A包含:( 1,1),(1,2),(2,1),(2,2)4个基本事件, (2分)
落在满足条件的区域内”的事件,事件A包含:( 1,1),(1,2),(2,1),(2,2)4个基本事件, (2分)
则
P(A) =![]() ; (2分)
; (2分)
(2)如图所示 ,![]() 可以看成平面中的点.试验的全部结果所构成的区域为:
可以看成平面中的点.试验的全部结果所构成的区域为:
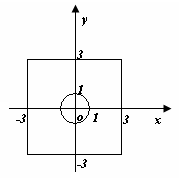 Ώ={(x,y)|
Ώ={(x,y)|![]() }, 面积为SΏ=36; (2分)
}, 面积为SΏ=36; (2分)
设B为“方程![]() 有两个实数根” 的事件,事件B所构成的区域为
有两个实数根” 的事件,事件B所构成的区域为
B={(x,y)|![]() ,Δ≥0},面积为SА=36 - ∏ ,这是一个几何概型, (2分)P(B)=
,Δ≥0},面积为SА=36 - ∏ ,这是一个几何概型, (2分)P(B)=![]() (2分)[
(2分)[


科目:高中数学 来源:2014届河北冀州中学高一下学期期中理科数学试卷(解析版) 题型:解答题
(本小题12分)已知函数 的图象在
的图象在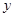 轴上的截距为1,在相邻两最值点
轴上的截距为1,在相邻两最值点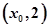 ,
,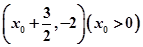 上
上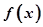 分别取得最大值和最小值.
分别取得最大值和最小值.
⑴求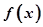 的解析式;
的解析式;
⑵若函数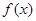 满足方程
满足方程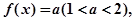 求在
求在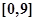 内的所有实数根之和.
内的所有实数根之和.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建师大附中高三上学期期中考试理科数学卷 题型:解答题
(本小题12分)已知函数 .
.
(I)若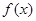 在
在 [1,+∞
[1,+∞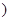 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;
(II)若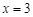 是
是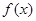 的极值点,求
的极值点,求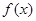 在
在 [1,a]上的最小值和最大值.
[1,a]上的最小值和最大值.
查看答案和解析>>
科目:高中数学 来源:2011-2012年浙江省高二第一学期期中考试理科数学 题型:解答题
((本小题12分)如图,在梯形 中,
中,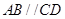 ,
, ,四边形
,四边形 为矩形,平面
为矩形,平面 平面
平面 ,
, .
.
(1)求证: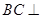 平面
平面 ;
;
(2)求二面角A-BF-C的平面角的余弦值;
(3)若点 在线段
在线段 上运动,设平面
上运动,设平面 与平面
与平面 所成二面角的平面角为
所成二面角的平面角为 ,试求
,试求 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源:2010-2011年河南省卫辉市高二4月月考数学理卷 题型:解答题
((本小题12分)
设函数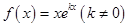
(1)求曲线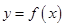 在点
在点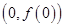 处的切线方程。
处的切线方程。
(2)若函数 在区间
在区间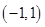 内单调递增,求
内单调递增,求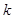 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com