练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数．如下定义一列函数：f1（x）=f（x），f2（x）=f（f1（x）），f3（x）=f（f2（x）），…，fn（x）=f（fn-1（x）），…，n∈N*，那么由归纳推理可得函数fn（x）的解析式是fn（x）=    ．
    【答案】分析：分别计算出f1（x），f2（x），f3（x），…，分析不等式的构成，寻找规律，进行归纳．
    解答：解：∵函数，
    f1（x）=f（x）=，
    f2（x）=f（f1（x））=，
    f3（x）=f（f2（x））=，
    f4（x）=f（f3（x））=，
    …
    所给的函数式的分子不变都是x，
    而分母是由两部分的和组成，
    第一部分的系数分别是1，3，7，15…2n-1，
    第二部分的数分别是2，4，8，16…2n
    ∴fn（x）=f（fn-1（x））=
    故答案为：．
    点评：本题考查归纳推理，实际上可看作给出一个数列的前几项写出数列的通项公式．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2013•镇江一模）已知函数f(x)=
    x2
    x2-x+1
    ，对一切正整数n，数列{an}定义如下：a1=
    1
    2
    ，且an+1=f（an），前n项和为Sn．
    （1）求函数f（x）的单调区间，并求值域；
    （2）证明{x|f（x）=x}={x|f（f（x））=x}；
    （3）对一切正整数n，证明：①an+1＜an；②Sn＜1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•许昌二模）已知函数f(x)=
    x
    x+2
    (x＞0)    ．如下定义一列函数：f1（x）=f（x），f2（x）=f（f1（x）），f3（x）=f（f2（x）），…，fn（x）=f（fn-1（x）），…，n∈N*，那么由归纳推理可得函数fn（x）的解析式是fn（x）=
    x
    (2n-1)x+2n
    x
    (2n-1)x+2n
    ．

    查看答案和解析>>

    科目：高中数学 来源：荆门市2008届高三数学试题(理)模拟训练题 题型：022

    有如下四个命题：

    ①已知函数(b为实常数，e是自然对数的底数)，若f(x)在区间[1，＋∞)内为减函数，则b的取值范围是(0，＋∞)．

    ②已知点A(x1，y1)，B(x2，y2)是函数y＝sinx(－π＜x＜0)图象上的两个不同点，则一定有；

    ③已知f(x)是定义在R上的不恒为零的函数，且对于任意的a，b∈R，满足：f(ab)＝af(b)＋bf(a)，f(2)＝2，an＝(n∈N*)，则数列{an}一定为等差数列

    ④已知O是△ABC所在平面上一定点，动点P满足：．则P点的轨迹一定通过△ABC的重心其中正确命题的序号为________

    查看答案和解析>>

    科目：高中数学 来源：河南省同步题 题型：填空题

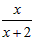    已知函数f（x）=（x>0），如下定义一列函数：f1（x）=f（x），f2（x）=f（f1（x）），f3（x）=f（f2（x）），……，fn（x）=f（fn-1 （x）），……，n∈N*，那么由归纳推理fn（x）可得函数的解析式是fn（x）=（    ）。

    查看答案和解析>>

    同步练习册答案