
【题目】已知集合A={x|x=a0+a1×2+a2×22+a3×23},其中ai∈{0,1,2}(i=0,1,2,3),且a0≠0,则A中所有元素之和等于 .
【答案】837
【解析】解:由题意可知,a3 , a1 , a2各有3种取法(均可取0,1,2),a0有2种取法,
由分步计数原理可得共有3×3×3×2种方法
∴当a0取1,2时,a1 , a2 , a3各有3种取法,共有3×3×3=27种方法,
即集合A中含有a0项的所有数的和为(1+2)×27=81;
同理可得集合A中含有a1项的所有数的和为(2×0+2×1+2×2)×18=108;
集合A中含有a2项的所有数的和为(22×0+22×1+22×2)×18=216;
集合A中含有a3项的所有数的和为(23×0+23×1+23×2)×18=432;
由分类计数原理得集合A中所有元素之和:
S=81+108+216+432=837.
所以答案是:837.
【考点精析】利用集合的表示方法-特定字母法对题目进行判断即可得到答案,需要熟知①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合.③描述法:{![]() |
|![]() 具有的性质},其中
具有的性质},其中![]() 为集合的代表元素.④图示法:用数轴或韦恩图来表示集合.
为集合的代表元素.④图示法:用数轴或韦恩图来表示集合.


科目:高中数学 来源: 题型:
【题目】我校要从参加数学竞赛的1000名学生中,随机抽取50名学生的成绩进行分析,现将参加数学竞赛的1000名学生编号如下000,001,002,…,999,如果在第一组随机抽取的一个号码为015,则抽取的第40个号码为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解高三年级学生寒假期间的学习情况,某学校抽取了甲、乙两班作为对象,调查这两个班的学生在寒假期间平均每天学习的时间(单位:小时),统计结果绘成频率分布直方图(如图).已知甲、乙两班学生人数相同,甲班学生平均每天学习时间在区间![]() 的有8人.
的有8人.
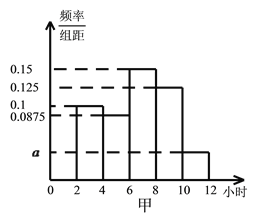

(I)求直方图中![]() 的值及甲班学生平均每天学习时间在区间
的值及甲班学生平均每天学习时间在区间![]() 的人数;
的人数;
(II)从甲、乙两个班平均每天学习时间大于10个小时的学生中任取4人参加测试,设4人中甲班学生的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了了解全校学生的上网情况,在全校采取随机抽样的方法抽取了![]() 名学生(其中男女生人数恰好各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月上网次数分为
名学生(其中男女生人数恰好各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月上网次数分为![]() 组:
组: ![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
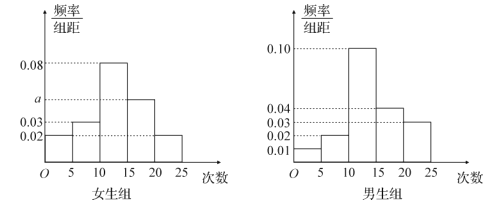
(1)写出![]() 的值;
的值;
(2)求抽取的![]() 名学生中月上网次数不少于
名学生中月上网次数不少于![]() 次的学生的人数;
次的学生的人数;
(3)在抽取的![]() 名学生中,从月上网次数少于
名学生中,从月上网次数少于![]() 次的学生中随机抽取
次的学生中随机抽取![]() 人,求至少抽取到
人,求至少抽取到![]() 名男生的概率.
名男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为 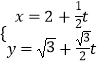 (t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρ=2.
(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρ=2.
(1)若点M的直角坐标为(2, ![]() ),直线l与曲线C1交于A、B两点,求|MA|+|MB|的值.
),直线l与曲线C1交于A、B两点,求|MA|+|MB|的值.
(2)设曲线C1经过伸缩变换 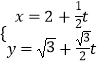 得到曲线C2 , 求曲线C2的内接矩形周长的最大值.
得到曲线C2 , 求曲线C2的内接矩形周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若a,b∈[﹣1,1],a+b≠0时,有 ![]() >0成立. (Ⅰ)判断f(x)在[﹣1,1]上的单调性,并证明;
>0成立. (Ⅰ)判断f(x)在[﹣1,1]上的单调性,并证明;
(Ⅱ)解不等式:f(2x﹣1)<f(1﹣3x);
(Ⅲ)若f(x)≤m2﹣2am+1对所有的a∈[﹣1,1]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明“当n为正奇数时,xn+yn能被x+y整除”,第二步归纳假设应写成( )
A.假设n=2k+1(k∈N*)正确,再推n=2k+3正确
B.假设n=2k﹣1(k∈N*)正确,再推n=2k+1正确
C.假设n=k(k∈N*)正确,再推n=k+1正确
D.假设n=k(k≥1)正确,再推n=k+2正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com