
【题目】如图,已知![]() 垂直于梯形
垂直于梯形![]() 所在的平面,
所在的平面,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .若四边形
.若四边形![]() 为矩形,线段
为矩形,线段![]() 与
与![]() 交于点
交于点![]() .
.

(1)证明:![]() ∥平面
∥平面![]() .
.
(2)求二面角![]() 的大小。
的大小。
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ?若存在,请求出
?若存在,请求出![]() 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
【答案】(1)详见解析;(2)![]() (3)在线段
(3)在线段![]() 上存在一点
上存在一点![]() ,且
,且![]()
【解析】
试题(1)连接![]() 在
在![]() 中,由题设知
中,由题设知![]() 分别为
分别为![]() 中点,所以
中点,所以![]() 由此可证
由此可证![]() // 平面
// 平面![]() ;
;
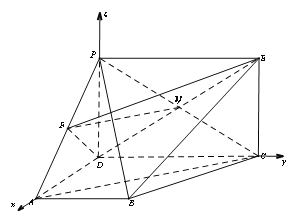
(2)如图以![]() 为原点,分别以
为原点,分别以![]() 所在直线为x,y,z轴,建立空间直角坐标系
所在直线为x,y,z轴,建立空间直角坐标系![]() 利用空间向量的数量积求出平面ABC和平面PBC的法向量的坐标,由法向量的夹角公式求出求二面角
利用空间向量的数量积求出平面ABC和平面PBC的法向量的坐标,由法向量的夹角公式求出求二面角![]() 的大小;
的大小;
(3)首先假设存在点Q满足条件.由![]() 设
设![]() ,再利用向量的夹角公式确定
,再利用向量的夹角公式确定![]() 的值.
的值.
试题解析:解:(Ⅰ)连接![]() 在
在![]() 中,
中,![]() 分别为
分别为![]() 中点,所以
中点,所以![]()
因为![]()
所以![]() 4分
4分
(2)如图以![]() 为原点,分别以
为原点,分别以![]() 所在直线为x,y,z轴,建立空间直角坐标系
所在直线为x,y,z轴,建立空间直角坐标系![]() 5分
5分
则![]()
设平面![]() 的法向量为
的法向量为![]() 则
则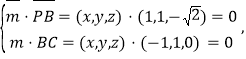
即![]() 解得
解得![]()
令![]() ,得
,得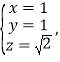 所以
所以![]() 7分
7分
因为平![]()
所以![]() ,
,
由图可知二面角![]() 为锐二面角,
为锐二面角,
所以二面角![]() 的大小为
的大小为![]() 9分
9分
(3)设存在点Q满足条件.
由![]() 设
设![]() ,
,
整理得![]() ,
,![]() 11分
11分
因为直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ,
,
所以![]() , 13分
, 13分
则![]() 知
知![]() ,即
,即![]() 点与E点重合.
点与E点重合.
故在线段![]() 上存在一点
上存在一点![]() ,且
,且![]() 14分
14分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】(.(12分)在一次购物抽奖活动中,假设某10张券中有一等奖奖券1张,可获价值50元的奖品;有二等奖奖券3张,每张可获价值10元的奖品;其余6张没奖。某顾客从此10张奖券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值X(元)的概率分布列。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2,对任意的x∈[t,t+2]不等式f(x+t)≥2f(x)恒成立,那么实数t的取值范围是( )
A. [![]() ,+∞) B. [2,+∞) C. (0,
,+∞) B. [2,+∞) C. (0,![]() ] D. [0,
] D. [0,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名运动员进行射击训练,已知他们击中的环数都稳定在![]() 、
、![]() 、
、![]() 、
、![]() 环,且每次射击成绩互不影响.根据以往的统计数据,甲、乙射击环数的频率分布条形图如下:
环,且每次射击成绩互不影响.根据以往的统计数据,甲、乙射击环数的频率分布条形图如下:
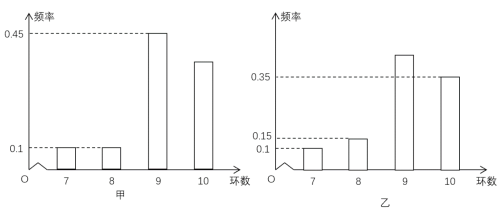
若将频率视为概率,回答下列问题:
(1)甲、乙各射击一次,求甲、乙同时击中![]() 环的概率;
环的概率;
(2)求甲射击一次,击中![]() 环以上(含
环以上(含![]() 环)的概率;
环)的概率;
(3)甲射击![]() 次,
次,![]() 表示这
表示这![]() 次射击中击中
次射击中击中![]() 环以上(含
环以上(含![]() 环)的次数,求
环)的次数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设n为给定的大于2的整数。有n个外表上没有区别的袋子,第k(k=1,2,···,n)个袋中有k个红球,n-k个白球。将这些袋子混合后,任选一个袋子,并且从中连续取出三个球(每次取出不放回)。求第三次取出的为白球的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com