
ЁОЬтФПЁПМзЁЂввСНУћдЫЖЏдБНјааЩфЛїбЕСЗЃЌвбжЊЫћУЧЛїжаЕФЛЗЪ§ЖМЮШЖЈдк![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЛЗЃЌЧвУПДЮЩфЛїГЩМЈЛЅВЛгАЯьЃЎИљОнвдЭљЕФЭГМЦЪ§ОнЃЌМзЁЂввЩфЛїЛЗЪ§ЕФЦЕТЪЗжВМЬѕаЮЭМШчЯТЃК
ЛЗЃЌЧвУПДЮЩфЛїГЩМЈЛЅВЛгАЯьЃЎИљОнвдЭљЕФЭГМЦЪ§ОнЃЌМзЁЂввЩфЛїЛЗЪ§ЕФЦЕТЪЗжВМЬѕаЮЭМШчЯТЃК
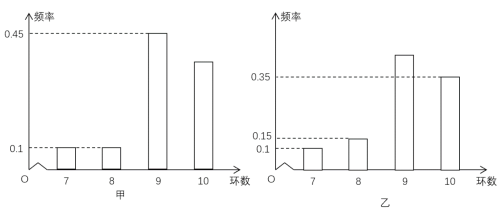
ШєНЋЦЕТЪЪгЮЊИХТЪЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉМзЁЂввИїЩфЛївЛДЮЃЌЧѓМзЁЂввЭЌЪБЛїжа![]() ЛЗЕФИХТЪЃЛ
ЛЗЕФИХТЪЃЛ
ЃЈ2ЃЉЧѓМзЩфЛївЛДЮЃЌЛїжа![]() ЛЗвдЩЯЃЈКЌ
ЛЗвдЩЯЃЈКЌ![]() ЛЗЃЉЕФИХТЪЃЛ
ЛЗЃЉЕФИХТЪЃЛ
ЃЈ3ЃЉМзЩфЛї![]() ДЮЃЌ
ДЮЃЌ![]() БэЪОет
БэЪОет![]() ДЮЩфЛїжаЛїжа
ДЮЩфЛїжаЛїжа![]() ЛЗвдЩЯЃЈКЌ
ЛЗвдЩЯЃЈКЌ![]() ЛЗЃЉЕФДЮЪ§ЃЌЧѓ
ЛЗЃЉЕФДЮЪ§ЃЌЧѓ![]() ЕФЗжВМСаМАЪ§бЇЦкЭћ
ЕФЗжВМСаМАЪ§бЇЦкЭћ![]() ЃЎ
ЃЎ
ЁОД№АИЁП(1) ![]() ;(2)
;(2) ![]() (3)МћНтЮі.
(3)МћНтЮі.
ЁОНтЮіЁП
(1)ЗжБ№МЦЫуГіМзввИїЩфЛївЛДЮЛїжа10ЛЗЕФИХТЪ,РћгУЯрЛЅЖРСЂЪТМўЕФИХТЪЙЋЪНМЦЫуМДПЩ;
(2)МзЩфЛївЛДЮ,Лїжа![]() ЛЗвдЩЯЃЈКЌ
ЛЗвдЩЯЃЈКЌ![]() ЛЗЃЉМДЮЊМзЩфЛївЛДЮ,Лїжа
ЛЗЃЉМДЮЊМзЩфЛївЛДЮ,Лїжа![]() ЛЗКЭМзЩфЛївЛДЮ,Лїжа10ЛЗ,РћгУЛЅГтЪТМўЕФИХТЪЙЋЪНМДПЩЕУГіНсЙћ;
ЛЗКЭМзЩфЛївЛДЮ,Лїжа10ЛЗ,РћгУЛЅГтЪТМўЕФИХТЪЙЋЪНМДПЩЕУГіНсЙћ;
(3)гЩ(2)ПЩжЊМзЩфЛївЛДЮЃЌЛїжа![]() ЛЗвдЩЯЃЈКЌ
ЛЗвдЩЯЃЈКЌ![]() ЛЗЃЉЕФИХТЪЮЊ0.8,ПЩжЊ
ЛЗЃЉЕФИХТЪЮЊ0.8,ПЩжЊ![]() .РћгУЙЋЪНМЦЫуМДПЩЕУГіНсЙћ.
.РћгУЙЋЪНМЦЫуМДПЩЕУГіНсЙћ.
(1) ЩшЪТМўAБэЪОМздЫЖЏдБЩфЛївЛДЮ,ЧЁКУЛїжа10ЛЗ, ЩшЪТМўBБэЪОввдЫЖЏдБЩфЛївЛДЮ,ЧЁКУЛїжа10ЛЗ, ![]() ,
,![]() ,ЫљвдМзЁЂввИїЩфЛївЛДЮ,МзЁЂввЭЌЪБЛїжа
,ЫљвдМзЁЂввИїЩфЛївЛДЮ,МзЁЂввЭЌЪБЛїжа![]() ЛЗМД
ЛЗМД![]() .
.
(2)ЩшЪТМўCБэЪОМздЫЖЏдБЩфЛївЛДЮ,ЧЁКУЛїжа9ЛЗвдЩЯ(КЌ9ЛЗ),дђ![]()
ЃЈ3ЃЉгЩвбжЊПЩЕУXЕФПЩФмШЁжЕЮЊ0,1,2,3,Чв![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]()
X | 0 | 1 | 2 | 3 |
P | 0.008 | 0.096 | 0.384 | 0.512 |
Ыљвд![]()


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕу![]() ЃЌ
ЃЌ![]() ЪЧвд
ЪЧвд![]() ЮЊЕзБпЕФЕШбќШ§НЧаЮЃЌЕу
ЮЊЕзБпЕФЕШбќШ§НЧаЮЃЌЕу![]() дкжБЯп
дкжБЯп![]() :
:![]() ЩЯЃЎ
ЩЯЃЎ
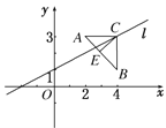
ЃЈ1ЃЉЧѓ![]() БпЩЯЕФИп
БпЩЯЕФИп![]() ЫљдкжБЯпЕФЗНГЬЃЛ
ЫљдкжБЯпЕФЗНГЬЃЛ
ЃЈ2ЃЉЧѓ![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ![]() ЃЌeЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЎ
ЃЌeЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЎ
ЃЈ1ЃЉШчЙћКЏЪ§![]() дк(0ЃЌ
дк(0ЃЌ![]() )ЩЯЕЅЕїЕндіЃЌЧѓmЕФШЁжЕЗЖЮЇЃЛ
)ЩЯЕЅЕїЕндіЃЌЧѓmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєжБЯп![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЭМЯѓЕФвЛЬѕЧаЯпЃЌЧѓЪЕЪ§kЕФжЕЃЛ
ЭМЯѓЕФвЛЬѕЧаЯпЃЌЧѓЪЕЪ§kЕФжЕЃЛ
ЃЈ3ЃЉЩш![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() ДЙжБгкЬнаЮ
ДЙжБгкЬнаЮ![]() ЫљдкЕФЦНУцЃЌ
ЫљдкЕФЦНУцЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЃЌ
ЃЌ![]() .ШєЫФБпаЮ
.ШєЫФБпаЮ![]() ЮЊОиаЮЃЌЯпЖЮ
ЮЊОиаЮЃЌЯпЖЮ![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() .
.

ЃЈ1ЃЉжЄУїЃК![]() ЁЮЦНУц
ЁЮЦНУц![]() .
.
ЃЈ2ЃЉЧѓЖўУцНЧ![]() ЕФДѓаЁЁЃ
ЕФДѓаЁЁЃ
ЃЈ3ЃЉдкЯпЖЮ![]() ЩЯЪЧЗёДцдквЛЕу
ЩЯЪЧЗёДцдквЛЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФДѓаЁЮЊ
ЫљГЩНЧЕФДѓаЁЮЊ![]() ЃПШєДцдкЃЌЧыЧѓГі
ЃПШєДцдкЃЌЧыЧѓГі![]() ЕФГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
ЕФГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЬтЮФЃЉШчЭМдкШ§РтзЖ![]() жаЃЌ
жаЃЌ ![]() ЗжБ№ЮЊРт
ЗжБ№ЮЊРт![]() ЕФжаЕуЃЌвбжЊ
ЕФжаЕуЃЌвбжЊ![]() ЃЌ
ЃЌ

ЧѓжЄЃКЃЈ1ЃЉжБЯп![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЦНУц![]()
![]() ЦНУц
ЦНУц![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁО2018КЃФЯИпШ§НзЖЮадВтЪдЃЈЖўФЃЃЉЁПШчЭМЃЌдкжБШ§Ртжљ![]() жаЃЌ
жаЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() ЮЊ
ЮЊ![]() ЩЯвЛЖЏЕуЃЎ
ЩЯвЛЖЏЕуЃЎ

ЃЈIЃЉЪЧЗёДцдквЛЕу![]() ЃЌЪЙЕУЯпЖЮ
ЃЌЪЙЕУЯпЖЮ![]() ЦНУц
ЦНУц![]() ЃПШєДцдкЃЌжИГіЕу
ЃПШєДцдкЃЌжИГіЕу![]() ЕФЮЛжУЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФЮЛжУЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈIIЃЉШєЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЧв
ЕФжаЕуЧв![]() ЃЌЧѓШ§РтзЖ
ЃЌЧѓШ§РтзЖ![]() ЕФЬхЛ§ЃЎ
ЕФЬхЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЫФБпаЮ![]() ЮЊжБНЧЬнаЮЃЌ
ЮЊжБНЧЬнаЮЃЌ![]() ЮЊОиаЮЃЌЦНУц
ЮЊОиаЮЃЌЦНУц![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ![]() ЁЮ
ЁЮ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
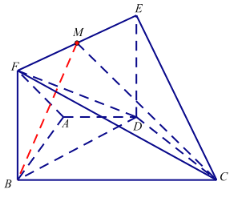
ЃЈ1ЃЉШєЕу![]() ЮЊ
ЮЊ![]() жаЕуЃЌЧѓжЄЃК
жаЕуЃЌЧѓжЄЃК![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯвЛЖЏЕуЃЌЧѓ
ЩЯвЛЖЏЕуЃЌЧѓ![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФШЁжЕЗЖЮЇЃЎ
ЫљГЩНЧЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДгМЏКЯ![]() жаЩОШЅ
жаЩОШЅ![]() ИіЪ§ЃЌЪЙЕУЪЃЯТЕФдЊЫижаЃЌШЮСНИіЪ§жЎКЭОљВЛЮЊ2015ЕФвђЪ§ЁЃЧѓ
ИіЪ§ЃЌЪЙЕУЪЃЯТЕФдЊЫижаЃЌШЮСНИіЪ§жЎКЭОљВЛЮЊ2015ЕФвђЪ§ЁЃЧѓ![]() ЕФзюаЁжЕЁЃ
ЕФзюаЁжЕЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФзѓЁЂгвНЙЕуЗжБ№ЮЊF1ЃЌF2ЃЌРыаФТЪ
ЕФзѓЁЂгвНЙЕуЗжБ№ЮЊF1ЃЌF2ЃЌРыаФТЪ![]() ЃЌЧвЭждВЕФЖЬжсГЄЮЊ2ЃЎ
ЃЌЧвЭждВЕФЖЬжсГЄЮЊ2ЃЎ
ЃЈ1ЃЉЧѓЭждВЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉвбжЊжБЯпl1ЃЌl2Й§гвНЙЕуF2ЃЌЧвЫќУЧЕФаБТЪГЫЛ§ЮЊЉ1ЃЌЩшl1ЃЌl2ЗжБ№гыЭждВНЛгкЕуAЃЌBКЭCЃЌDЃЎЂйЧѓABЃЋCDЕФжЕЃЛЂкЩшABЕФжаЕуMЃЌCDЕФжаЕуЮЊNЃЌЧѓЁїOMNУцЛ§ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com