
【题目】已知函数![]() ,
,![]() .
.![]() ,e为自然对数的底数.
,e为自然对数的底数.
(1)如果函数![]() 在(0,
在(0,![]() )上单调递增,求m的取值范围;
)上单调递增,求m的取值范围;
(2)若直线![]() 是函数
是函数![]() 图象的一条切线,求实数k的值;
图象的一条切线,求实数k的值;
(3)设![]() ,
,![]() ,且
,且![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)1(3)见解析。
(2)1(3)见解析。
【解析】
(1)依题意h′(x)=ex﹣2mx≥0(0,+∞)上恒成立.即![]() 在(0,+∞)上恒成立.即求函数
在(0,+∞)上恒成立.即求函数![]() 的最小值即可;(2)设切点
的最小值即可;(2)设切点![]() ,则切线方程为则
,则切线方程为则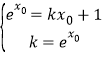 进而得到
进而得到![]() ,令
,令![]() 对函数求导得到函数的单调性和零点即可得到k值(3):要证
对函数求导得到函数的单调性和零点即可得到k值(3):要证![]() ,只要证
,只要证![]() ,两边同时除以
,两边同时除以![]() 令x2﹣x1=t,t>0,即证(t﹣2)et+t+2>0,利用
令x2﹣x1=t,t>0,即证(t﹣2)et+t+2>0,利用![]() =(t﹣2)et+t+2,(t>0)单调性即可证明
=(t﹣2)et+t+2,(t>0)单调性即可证明
:(1)![]() ,
,![]()
要使![]() 在
在![]() 上单调递增,则
上单调递增,则![]() 在
在![]() 上恒成立.
上恒成立.
∴![]() ,∴
,∴![]() ,令
,令![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
∴当x=1时,![]() 有最小值为
有最小值为![]() ,∴
,∴![]()
(2)∵![]() ,∴
,∴![]() ,设切点为
,设切点为![]() ,则
,则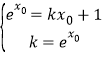
∴![]() ,令
,令![]() ,
,![]()
∴![]() 时,
时,![]() ,
,![]() 单调递减,当k>1时,
单调递减,当k>1时,![]() ,
,![]() 单调递增
单调递增
∴k=1时,![]() ,∴
,∴![]() 时,k=1.∴实数k的值为1.
时,k=1.∴实数k的值为1.
(3)要证![]()
只要证![]() ,两边同时除以
,两边同时除以![]() 得:
得:
![]() ,令
,令![]() 得:
得:![]()
所以只要证:![]() ,令
,令![]()
∴![]() ,
,![]() ,∴
,∴![]()
即![]() ,∴原不等式成立.
,∴原不等式成立.


科目:高中数学 来源: 题型:
【题目】甲乙两个同学进行定点投篮游戏,已知他们每一次投篮投中的概率均为![]() ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
(1)求甲同学至少有4次投中的概率;
(2)求乙同学投篮次数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(.(12分)在一次购物抽奖活动中,假设某10张券中有一等奖奖券1张,可获价值50元的奖品;有二等奖奖券3张,每张可获价值10元的奖品;其余6张没奖。某顾客从此10张奖券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值X(元)的概率分布列。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名运动员进行射击训练,已知他们击中的环数都稳定在![]() 、
、![]() 、
、![]() 、
、![]() 环,且每次射击成绩互不影响.根据以往的统计数据,甲、乙射击环数的频率分布条形图如下:
环,且每次射击成绩互不影响.根据以往的统计数据,甲、乙射击环数的频率分布条形图如下:
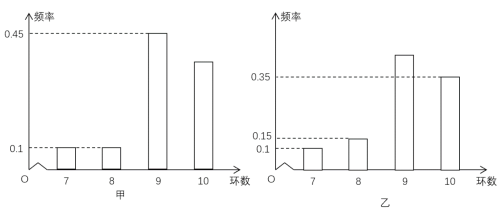
若将频率视为概率,回答下列问题:
(1)甲、乙各射击一次,求甲、乙同时击中![]() 环的概率;
环的概率;
(2)求甲射击一次,击中![]() 环以上(含
环以上(含![]() 环)的概率;
环)的概率;
(3)甲射击![]() 次,
次,![]() 表示这
表示这![]() 次射击中击中
次射击中击中![]() 环以上(含
环以上(含![]() 环)的次数,求
环)的次数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com