
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,且函数
,且函数![]() 只有一个零点,求
只有一个零点,求![]() 的最小值.
的最小值.
【答案】(1)答案不唯一,具体见解析(2)![]() 的最小值为1
的最小值为1
【解析】
(1)首先求出函数的定义域与导函数,讨论![]() 的取值范围,分别求出函数的单调区间即可.
的取值范围,分别求出函数的单调区间即可.
(2)解法一:问题等价于![]() 只有一个交点,令
只有一个交点,令![]() ,可得
,可得![]() ,记
,记![]() ,讨论
,讨论![]() 的取值,确定方程根的个数即可求解;解法二:问题等价于
的取值,确定方程根的个数即可求解;解法二:问题等价于![]() 只有一个交点,令
只有一个交点,令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,记
,记![]() ,作出函数
,作出函数![]() 和函数
和函数![]() 的图像,利用图像的交点即可求解.
的图像,利用图像的交点即可求解.
解:(1)由题意可知![]() ,
,![]() .
.
当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)解法一:由题意可知![]() ,且
,且![]() .
.
令![]() ,
,
则![]() .
.
记![]() ,(*)
,(*)
当![]() 时,
时,![]() ,与
,与![]() 相矛盾,此时(*)式无解;
相矛盾,此时(*)式无解;
当![]() 时,
时,![]() 无解;
无解;
当![]() 时,(*)式的解为
时,(*)式的解为![]() ,此时
,此时![]() 有唯一解
有唯一解![]() ;
;
当![]() 时,
时,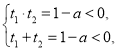
![]() ,
,
所以(*)式只有一个负根![]() ,
,![]() 有唯一解,故
有唯一解,故![]() 的最小值为1.
的最小值为1.
解法二:由题得![]() ,
,
令![]() ,则
,则![]() .
.
再令![]() ,则
,则![]() .
.
记![]() ,
,
函数![]() 和函数
和函数![]() 的图象如图所示:
的图象如图所示:
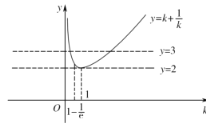
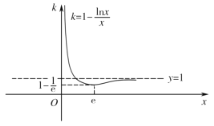
当![]() ,即
,即![]() 时,显然不成立;
时,显然不成立;
当![]() ,即
,即![]() 时,由
时,由![]() ,得方程
,得方程![]() 存在唯一解
存在唯一解![]() ,且
,且![]() .
.
此时![]() 亦存在唯一解
亦存在唯一解![]() .
.
综上,![]() 的最小值为1.
的最小值为1.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】若![]() 、
、![]() 是两个相交平面,则在下列命题中,真命题的序号为( )
是两个相交平面,则在下列命题中,真命题的序号为( )
①若直线![]() ,则在平面
,则在平面![]() 内一定不存在与直线
内一定不存在与直线![]() 平行的直线.
平行的直线.
②若直线![]() ,则在平面
,则在平面![]() 内一定存在无数条直线与直线
内一定存在无数条直线与直线![]() 垂直.
垂直.
③若直线![]() ,则在平面
,则在平面![]() 内不一定存在与直线
内不一定存在与直线![]() 垂直的直线.
垂直的直线.
④若直线![]() ,则在平面
,则在平面![]() 内一定存在与直线
内一定存在与直线![]() 垂直的直线.
垂直的直线.
A. ①③ B. ②③ C. ②④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电信公司为了加强新用5G技术的推广使用,为该公司的用户制定了一套5G月消费返流量费的套餐服务方案;当月消费金额不超过100元时,按消费金额的![]() 进行返还;当月消费金额超过100元时,除消费金额中的100元仍按
进行返还;当月消费金额超过100元时,除消费金额中的100元仍按![]() 进行返还外,若另超出100元的部分消费金额为A元,则超过部分按
进行返还外,若另超出100元的部分消费金额为A元,则超过部分按![]() 进行返还,记用户当月返还所得流量费y(单位:元),消费金额x(单位:元)
进行返还,记用户当月返还所得流量费y(单位:元),消费金额x(单位:元)
(1)写出该公司用户月返还所得流量费的函数模型;
(2)如果用户小李当月获返还的流量费是12元,那么他这个月的消费金额是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了释放学生压力,某校高三年级一班进行了一个投篮游戏,其间甲、乙两人轮流进行篮球定点投篮比赛(每人各投一次为一轮).在相同的条件下,每轮甲乙两人站在同一位置,甲先投,每人投一次篮,两人有1人命中,命中者得1分,未命中者得-1分;两人都命中或都未命中,两人均得0分.设甲每次投篮命中的概率为![]() ,乙每次投篮命中的概率为
,乙每次投篮命中的概率为![]() ,且各次投篮互不影响.
,且各次投篮互不影响.
(1)经过1轮投篮,记甲的得分为![]() ,求
,求![]() 的分布列及期望;
的分布列及期望;
(2)用![]() 表示经过第
表示经过第![]() 轮投篮后,甲的累计得分高于乙的累计得分的概率,求
轮投篮后,甲的累计得分高于乙的累计得分的概率,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘.如下图所示,从左到右有ABC三根柱子,其中A柱子上面有从小叠到大的n个圆盘,现要求将A柱子上的圆盘移到C柱子上去,期间只有一个原则:一次只能移动一个盘子且大盘子不能在小盘子上面,则移动的次数为_______(用![]() 表示)
表示)
A B
B C
C
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 与一等轴双曲线相交,
与一等轴双曲线相交,![]() 是其中一个交点,并且双曲线的顶点是该椭圆的焦点
是其中一个交点,并且双曲线的顶点是该椭圆的焦点![]() ,
,![]() ,双曲线的焦点是椭圆的左、右顶点,设
,双曲线的焦点是椭圆的左、右顶点,设![]() 为该双曲线上异于顶点的任意一点,直线
为该双曲线上异于顶点的任意一点,直线![]() 的斜率分别为
的斜率分别为![]() ,且直线
,且直线![]() 和
和![]() 与椭圆的交点分别为
与椭圆的交点分别为![]() 、
、![]() 和
和![]() 、
、![]() .
.

(1)求椭圆和双曲线的标准方程;
(2)(i)证明:![]() ;
;
(ii)是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.![]() ,e为自然对数的底数.
,e为自然对数的底数.
(1)如果函数![]() 在(0,
在(0,![]() )上单调递增,求m的取值范围;
)上单调递增,求m的取值范围;
(2)若直线![]() 是函数
是函数![]() 图象的一条切线,求实数k的值;
图象的一条切线,求实数k的值;
(3)设![]() ,
,![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com