
【题目】已知函数![]() ,
,![]() .
.
(1)求证:![]()
(2)若![]() 有两个零点,求
有两个零点,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)见解析.
【解析】
(1)计算![]() ,令
,令![]() ,进而由
,进而由![]() 可得
可得![]() 在
在![]() 上单调递增,分析导函数的正负可得存在
上单调递增,分析导函数的正负可得存在![]() ,使得
,使得![]() ,(*),即得
,(*),即得![]() ,从而得
,从而得![]() ,从而得证;
,从而得证;
(2)函数![]() 有两个零点等价于方程
有两个零点等价于方程![]() 有两个不同的解,又等价于
有两个不同的解,又等价于![]() 有两个不同的解,令
有两个不同的解,令![]() ,求导,分析函数的单调性和极值即可得解.
,求导,分析函数的单调性和极值即可得解.
(1)证明:![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递增,即
上单调递增,即![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,![]() ,
,
故存在![]() ,使得
,使得![]() ,(*)
,(*)
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
所以对![]() ,均有
,均有![]() ,①
,①
由(*)式可得![]() ,代入①式得
,代入①式得![]() ,
,
又![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() 时取“=”,但
时取“=”,但![]() ,故
,故![]() ,
,
故![]() .
.
(2)解:由题得![]() ,
,
于是函数![]() 有两个零点等价于方程
有两个零点等价于方程![]() 有两个不同的解,
有两个不同的解,
因为![]() ,所以又等价于
,所以又等价于![]() 有两个不同的解.
有两个不同的解.
令![]() ,则
,则![]() ,
,
再令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,所以当
,所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
故当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
于是当![]() 时,
时,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() 单调递增,即
单调递增,即![]() 是
是![]() 在
在![]() 上的最小值,
上的最小值,
于是,若![]() ,即
,即![]() 时,则当
时,则当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上至多有一个零点
上至多有一个零点![]() ;
;
若![]() ,即
,即![]() 时,则当
时,则当![]() 时,由于
时,由于![]() ,
,![]() ,
,
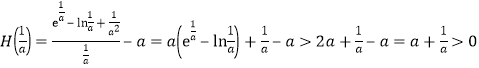 ,
,
故![]() 在
在![]() 上有且仅有一个零点
上有且仅有一个零点![]() ;
;
同理,当![]() 时,由于
时,由于![]() ,
,![]() ,
,
![]() ,
,
故![]() 在
在![]() 上有且仅有一个零点
上有且仅有一个零点![]() ,即当
,即当![]() 时,
时,![]() 共有两个零点
共有两个零点![]() .
.
综上,当![]() 时,
时,![]() 有两个零点.
有两个零点.


科目:高中数学 来源: 题型:
【题目】某电信公司为了加强新用5G技术的推广使用,为该公司的用户制定了一套5G月消费返流量费的套餐服务方案;当月消费金额不超过100元时,按消费金额的![]() 进行返还;当月消费金额超过100元时,除消费金额中的100元仍按
进行返还;当月消费金额超过100元时,除消费金额中的100元仍按![]() 进行返还外,若另超出100元的部分消费金额为A元,则超过部分按
进行返还外,若另超出100元的部分消费金额为A元,则超过部分按![]() 进行返还,记用户当月返还所得流量费y(单位:元),消费金额x(单位:元)
进行返还,记用户当月返还所得流量费y(单位:元),消费金额x(单位:元)
(1)写出该公司用户月返还所得流量费的函数模型;
(2)如果用户小李当月获返还的流量费是12元,那么他这个月的消费金额是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 与一等轴双曲线相交,
与一等轴双曲线相交,![]() 是其中一个交点,并且双曲线的顶点是该椭圆的焦点
是其中一个交点,并且双曲线的顶点是该椭圆的焦点![]() ,
,![]() ,双曲线的焦点是椭圆的左、右顶点,设
,双曲线的焦点是椭圆的左、右顶点,设![]() 为该双曲线上异于顶点的任意一点,直线
为该双曲线上异于顶点的任意一点,直线![]() 的斜率分别为
的斜率分别为![]() ,且直线
,且直线![]() 和
和![]() 与椭圆的交点分别为
与椭圆的交点分别为![]() 、
、![]() 和
和![]() 、
、![]() .
.

(1)求椭圆和双曲线的标准方程;
(2)(i)证明:![]() ;
;
(ii)是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 上的点,
上的点,![]() ,且
,且![]() (①).将四边形
(①).将四边形![]() 沿
沿![]() 折起,连接
折起,连接![]() (②).在折起的过程中,下列说法中正确的是( )
(②).在折起的过程中,下列说法中正确的是( )
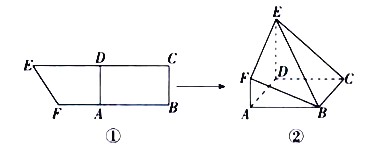
A.![]() 平面
平面![]()
B.![]() 四点不可能共面
四点不可能共面
C.若![]() ,则平面
,则平面![]() 平面
平面![]()
D.平面![]() 与平面
与平面![]() 可能垂直
可能垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.![]() ,e为自然对数的底数.
,e为自然对数的底数.
(1)如果函数![]() 在(0,
在(0,![]() )上单调递增,求m的取值范围;
)上单调递增,求m的取值范围;
(2)若直线![]() 是函数
是函数![]() 图象的一条切线,求实数k的值;
图象的一条切线,求实数k的值;
(3)设![]() ,
,![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com