
【题目】设等差数列![]() 是无穷数列,且各项均为互不相同的正整数,其前
是无穷数列,且各项均为互不相同的正整数,其前![]() 项和为
项和为![]() ,数列
,数列![]() 满足
满足![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若数列![]() 为等差数列,求
为等差数列,求![]() ;
;
(3)在(1)的条件下,求证:数列![]() 中存在无穷多项(按原来的顺序)成等比数列.
中存在无穷多项(按原来的顺序)成等比数列.
 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD为正方形, ![]() 为直角三角形,
为直角三角形, ![]() ,且
,且![]() .
.
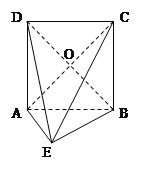
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若AB=2AE,求异面直线BE与AC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十二届全国人民代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)分别于2017年3月5日和3月3日在北京开幕,某高校学生会为了解该校学生对全国两会的关注情况,随机调查了该校200名学生,并将这200名学生分为对两会“比较关注”与“不太关注”两类,已知这200名学生中男生比女生多20人,对两会“比较关注”的学生中男生人数比女生人数之比为![]() ,对两会“不太关注”的学生中男生比女生少5人.
,对两会“不太关注”的学生中男生比女生少5人.
(Ⅰ)根据题意建立的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为男生与女生对两会的关注有差异?
的把握认为男生与女生对两会的关注有差异?
(Ⅱ)该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,再从这7人中随机选出2人参与两会宣传活动,求这2人全是男生的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
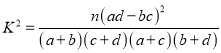 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的单调递减函数
上的单调递减函数![]() ,对任意
,对任意![]() 都有
都有![]() ,
, ![]() .
.
(Ⅰ)判断函数![]() 的奇偶性,并证明之;
的奇偶性,并证明之;
(Ⅱ)若对任意![]() ,不等式
,不等式![]() (
(![]() 为常实数)都成立,求
为常实数)都成立,求![]() 的取值范围;(Ⅲ)设
的取值范围;(Ⅲ)设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
若![]()
![]()
![]() ,
, ![]() ,比较
,比较![]() 的大小并说明理由.
的大小并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若存在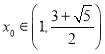 ,使函数
,使函数![]() 的图像在点
的图像在点![]() 和点
和点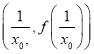 处的切线互相垂直,求
处的切线互相垂直,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 在区间
在区间![]() 上有两个极值点,则是否存在实数
上有两个极值点,则是否存在实数![]() ,使
,使![]() 对任意的
对任意的![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,我海监船在![]() 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至![]() 处,此时测得其东北方向与它相距32海里的
处,此时测得其东北方向与它相距32海里的![]() 处有一外国船只,且
处有一外国船只,且![]() 岛位于海监船正东
岛位于海监船正东![]() 海里处.
海里处.

(1)求此时该外国船只与![]() 岛的距离;
岛的距离;
(2)观测中发现,此外国船只正以每小时8海里的速度沿正南方向航行,为了将该船拦截在离![]() 岛24海里处,不让其进入
岛24海里处,不让其进入![]() 岛24海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:
岛24海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com