
【题目】已知![]() ,设函数
,设函数![]() .
.
(1)存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的最大值,求
上的最大值,求![]() 的取值范围;
的取值范围;
(2)![]() 对任意
对任意![]() 恒成立时,
恒成立时,![]() 的最大值为1,求
的最大值为1,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2) ![]() .
.
【解析】
试题分析:(1)求函数![]() 的导数得
的导数得![]() ,分别讨论
,分别讨论![]() 时函数
时函数![]() 在区间
在区间![]() 的最大值点是否符合题意即可;
的最大值点是否符合题意即可;
(2)![]() ,构造函数
,构造函数![]() ,道
,道![]() 的最大值为
的最大值为![]() ,等价于
,等价于![]() 在区间
在区间![]() 上恒成立,由于
上恒成立,由于![]() ,则
,则![]() ,此时
,此时![]() 恒成立,即
恒成立,即![]() 在区间
在区间![]() 上单调递增,符合题意.
上单调递增,符合题意.
试题解析:(1)![]() ,
,
①当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
∴![]() ,由
,由![]() ,得
,得![]() 在
在![]() 时无解,
时无解,
②当![]() 时,不合题意;
时,不合题意;
③当![]() 时,
时,![]() 在
在![]() 单调递增,在
单调递增,在![]() 递减,在
递减,在![]() 单调递增,
单调递增,
∴![]() 即
即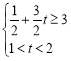 ,∴
,∴![]() ,
,
④当![]() 时,
时,![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,满足条件,
单调递减,满足条件,
综上所述:![]() 时,存在
时,存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的最大值.
上的最大值.
(2)![]() 对任意
对任意![]() 恒成立,
恒成立,
即![]() 对任意
对任意![]() 恒成立,令
恒成立,令
![]() ,
,![]() ,根据题意,可以知道
,根据题意,可以知道![]() 的最大值为1,则
的最大值为1,则
![]() 恒成立,
恒成立,
由于![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,若
,若![]() ,则
,则![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,则
上递增,则![]() ,∴
,∴![]() 在
在![]() 上是递增的函数.
上是递增的函数.
∴![]() ,满足条件,∴
,满足条件,∴![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,
, ![]() 是椭圆
是椭圆![]() 的右焦点,
的右焦点, ![]() 的斜率为
的斜率为![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,当
两点,当![]() 面积最大时,求
面积最大时,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国好声音(![]()
![]()
![]()
![]() )》是由浙江卫视联合星空传媒旗下灿星制作强力打造的大型励志专业音乐评论节目,于2012年7月13日在浙江卫视播出.每期节目有四位导师参加.导师背对歌手,当每位参赛选手演唱完之前有导师为其转身,则该选手可以选择加入为其转身的导师的团队中接受指导训练.已知某期《中国好声音》中,6位选手唱完后,四位导师为其转身的情况如下表所示:
)》是由浙江卫视联合星空传媒旗下灿星制作强力打造的大型励志专业音乐评论节目,于2012年7月13日在浙江卫视播出.每期节目有四位导师参加.导师背对歌手,当每位参赛选手演唱完之前有导师为其转身,则该选手可以选择加入为其转身的导师的团队中接受指导训练.已知某期《中国好声音》中,6位选手唱完后,四位导师为其转身的情况如下表所示:
导师转身人数(人) | 4 | 3 | 2 | 1 |
获得相应导师转身的选手人数(人) | 1 | 2 | 2 | 1 |
现从这6位选手中随机抽取两人考查他们演唱完后导师的转身情况.
(1)请列出所有的基本事件;
(2)求两人中恰好其中一位为其转身的导师不少于3人,而另一人为其转身的导师不多于2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)求证:曲线![]() 在点
在点![]() 处的切线过定点;
处的切线过定点;
(2)若![]() 是
是![]() 在区间
在区间![]() 上的极大值,但不是最大值,求实数
上的极大值,但不是最大值,求实数![]() 的取值范围;
的取值范围;
(3)求证:对任意给定的正数![]() ,总存在
,总存在![]() ,使得
,使得![]() 在
在![]() 上为单调函数.
上为单调函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 是无穷数列,且各项均为互不相同的正整数,其前
是无穷数列,且各项均为互不相同的正整数,其前![]() 项和为
项和为![]() ,数列
,数列![]() 满足
满足![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若数列![]() 为等差数列,求
为等差数列,求![]() ;
;
(3)在(1)的条件下,求证:数列![]() 中存在无穷多项(按原来的顺序)成等比数列.
中存在无穷多项(按原来的顺序)成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校男女篮球队各有10名队员,现将这20名队员的身高绘制成茎叶图(单位:![]() ).男队员身高在
).男队员身高在![]() 以上定义为“高个子”,女队员身高在
以上定义为“高个子”,女队员身高在![]() 以上定义为“高个子”,其他队员定义为“非高个子”,按照“高个子”和“非高个子”用分层抽样的方法共抽取5名队员.
以上定义为“高个子”,其他队员定义为“非高个子”,按照“高个子”和“非高个子”用分层抽样的方法共抽取5名队员.
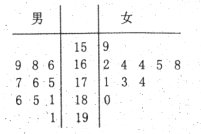
(1)从这5名队员中随机选出2名队员,求这2名队员中有“高个子”的概率;
(2)求这5名队员中,恰好男女“高个子”各1名队员的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,判断函数
,判断函数![]() 的单调性;
的单调性;
(2)若函数![]() 在定义域内单调递减,求实数
在定义域内单调递减,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,关于
时,关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com