
����Ŀ��Ϊ�����ļ����ºͶ�����ůʱ������Դ��ģ����ݵ��ݶ�����ǽ��Ҫ������Ȳ㣮ij��������Ҫ�����ʹ��20��ĸ��Ȳ㣬ÿ����ĸ��Ȳ㽨��ɱ�Ϊ6��Ԫ���ý�����ÿ�����Դ���ķ���C����λ����Ԫ������Ȳ���x����λ��cm�������ϵ��C��x��= ![]() ��0��x��10�������������Ȳ㣬ÿ����Դ���ķ���Ϊ8��Ԫ����f��x��Ϊ���Ȳ㽨�������20�����Դ���ķ���֮�ͣ�
��0��x��10�������������Ȳ㣬ÿ����Դ���ķ���Ϊ8��Ԫ����f��x��Ϊ���Ȳ㽨�������20�����Դ���ķ���֮�ͣ�
��1����k��ֵ��f��x���ı���ʽ��
��2�����Ȳ������ʱ���ܷ���f��x���ﵽ��С��������Сֵ��
���𰸡�
��1���⣺����Ȳ���Ϊxcm�������裬ÿ����Դ���ķ���Ϊ ![]() ��
��
����C��0��=8����k=40��
��� ![]() ��
��
���������ΪC1��x��=6x��
���ø��Ȳ㽨�������20�����Դ���ķ���֮��Ϊ
![]()
��2���⣺ ![]() ����f'��x��=0����
����f'��x��=0���� ![]() ��
��
���x=5�� ![]() ����ȥ����
����ȥ����
��0��x��5ʱ��f�䣨x����0����5��x��10ʱ��f�䣨x����0����x=5��f��x������Сֵ�㣬��Ӧ����СֵΪ ![]() ��
��
�����Ȳ���5cm��ʱ���ܷ��ôﵽ��СֵΪ70��Ԫ
����������1���ɽ�����ÿ�����Դ���ķ���C����λ����Ԫ������Ȳ���x����λ��cm�������ϵ��C��x��= ![]() �����������Ȳ㣬ÿ����Դ���ķ���Ϊ8��Ԫ�����ǿɵ�C��0��=8����k=40�������õ�
�����������Ȳ㣬ÿ����Դ���ķ���Ϊ8��Ԫ�����ǿɵ�C��0��=8����k=40�������õ� ![]() ���������ΪC1��x��=6x������ݸ��Ȳ㽨�������20�����Դ���ķ���֮��Ϊf��x�������Dz��ѵõ�f��x���ı���ʽ����2���ɣ�1���������f��x���ı���ʽ���������õ��������������f��x���ĵ����ԣ�Ȼ����ݺ���������������ܷ���f��x������Сֵ��
���������ΪC1��x��=6x������ݸ��Ȳ㽨�������20�����Դ���ķ���֮��Ϊf��x�������Dz��ѵõ�f��x���ı���ʽ����2���ɣ�1���������f��x���ı���ʽ���������õ��������������f��x���ĵ����ԣ�Ȼ����ݺ���������������ܷ���f��x������Сֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ��
�� ![]() .
.
��1�� ����![]() �ķ���
�ķ���![]() ������
������![]() ���н�,��
���н�,��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2�� ��![]() ʱ��
ʱ�� ![]() �����,��ʵ��
�����,��ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��ֱ������
��ֱ������![]() ��ֱ������
��ֱ������![]() ����ƽ��������ֱ��
����ƽ��������ֱ�� ![]() ����
����![]() ��
�� ![]() .
.
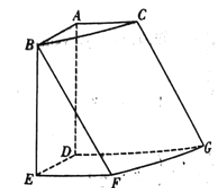
��1����֤�� ![]() �ĵ㹲�棻
�ĵ㹲�棻
��2��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ե�C��t�� ![]() ����t��R��t��0��ΪԲ�ĵ�Բ��ԭ��O��
����t��R��t��0��ΪԲ�ĵ�Բ��ԭ��O��
��1����ֱ��3x+y��4=0��ԲC���ڵ�M��N����|OM|=|ON|����ԲC�ķ��̣�
��2���ڣ�1���������£���B��0��2������P��Q�ֱ���ֱ��l��x+y+2=0��ԲC�ϵĶ��㣬��|PQ|��|PB|�����ֵ����ʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����к����У��뺯��y= ![]() ����ͬ��������ǣ� ��
����ͬ��������ǣ� ��
A.f��x��=lnx
B.![]()
C.f��x��=|x|
D.f��x��=ex
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() Ϊ������
������ ![]() ������
������![]() ��
�� ![]() ������
������![]() ����Ȼ�����ĵ�����.
����Ȼ�����ĵ�����.
��1��������ԭ��![]() ������
������![]() �����ߣ����е�Ϊ
�����ߣ����е�Ϊ![]() ����֤��
����֤�� ![]() ��
��
��2����![]() ��������
��������![]() ������
������![]() ���ǵ�����������
���ǵ�����������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���������ABC�У���֪AB=AC=1��A=120�㣬E��F�ֱ��DZ�AB��AC�ϵĵ㣬�� ![]() ��
�� ![]() ������m��n�ʣ�0��1������EF��BC���е�ֱ�ΪM��N����m+4n=1����
������m��n�ʣ�0��1������EF��BC���е�ֱ�ΪM��N����m+4n=1���� ![]() ����СֵΪ ��
����СֵΪ �� 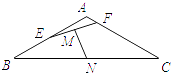
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�������ڽ�A��B��C���Եı߷ֱ�Ϊa��b��c���������ڽ�A��B��C�ɵȲ����У���a= ![]() ��b=
��b= ![]() ����sinC��ֵ��
����sinC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���������ŵ��������Σ����������кܶ���ɫʳƷ������ˮ��������������У���Զʯ����ɽ�桢���������19�֣�����������������У�һƷ����⡢��ī�֡��˹�ɽ��ȼݵ�38�֣�С��������������У����뼯�ռ�����ΪѬѼ���Ϸ���Ϻ��57�֣��������ŵ��ο;������ֲ�����ķ�������Щ�ز�����6�ִ�������Ʒ����
��1����Ӧ��ˮ���ࡢ�����ࡢС�����зֱ���ص�������
��2����ij�οʹ���ص�6���ز��������ȡ2�����Լ��ĸ�ĸ��
���г����п��ܵij�ȡ�����
�����ȡ��2���ز���ΪС�Եĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com