
已知数列{an}前n项和为Sn,且a2an=S2+Sn对一切正整数都成立.
(1)求a1,a2的值;
(2)设a1>0,数列 前n项和为Tn,当n为何值时,Tn最大?并求出最大值.
前n项和为Tn,当n为何值时,Tn最大?并求出最大值.
(1)a1=0,a2=0或a1=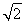 +1,a2=
+1,a2=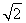 +2或a1=1-
+2或a1=1-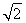 ,a2=2-
,a2=2-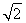 .(2)n=7时,Tn取得最大值,T7=7-
.(2)n=7时,Tn取得最大值,T7=7- lg2.
lg2.
【解析】(1)取n=1时,a2a1=S2+S1=2a1+a2,①
取n=2时,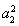 =2a1+2a2.②由②-①得,a2(a2-a1)=a2.③
=2a1+2a2.②由②-①得,a2(a2-a1)=a2.③
若a2=0,由①知a1=0;若a2≠0,由③知a2-a1=1.④
由①④解得a1= +1,a2=2+
+1,a2=2+ 或a1=1-
或a1=1-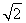 ,a2=2-
,a2=2- .
.
综上所述,a1=0,a2=0或a1=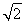 +1,a2=
+1,a2=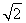 +2或a1=1-
+2或a1=1-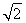 ,a2=2-
,a2=2-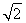 .
.
(2)当a1>0时,a1=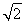 +1,a2=
+1,a2= +2.
+2.
n≥2时,有(2+ )an=S2+Sn,(2+
)an=S2+Sn,(2+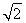 )an-1=S2+Sn-1,
)an-1=S2+Sn-1,
∴(1+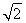 )an=(2+
)an=(2+ )an-1,即an=
)an-1,即an= an-1(n≥2),
an-1(n≥2),
∴an=a1( )n-1=(
)n-1=(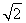 +1)(
+1)(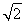 )n-1.令bn=
)n-1.令bn= =1-
=1-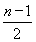 lg2,
lg2,
故{bn}是递减的等差数列,从而b1>b2>…>b7=lg >lg1=0,
>lg1=0,
n≥8时,bn≤b8= lg
lg <
< lg1=0,故n=7时,Tn取得最大值,T7=7-
lg1=0,故n=7时,Tn取得最大值,T7=7- lg2
lg2


科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第3课时练习卷(解析版) 题型:填空题
如图所示,b,c在平面α内,a∩c=B,b∩c=A,且a⊥b,a⊥c,b⊥c,若C∈a,D∈b,E在线段AB上(C、D、E均异于A、B),则△ACD的形状是________.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第1课时练习卷(解析版) 题型:解答题
如图,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BC∥=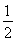 AD,BE∥=
AD,BE∥=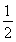 FA,G、H分别为FA、FD的中点.
FA,G、H分别为FA、FD的中点.
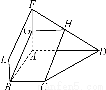
(1)证明:四边形BCHG是平行四边形.
(2)C、D、F、E四点是否共面?为什么?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(解析版) 题型:解答题
已知数列{an}中,a1=2,n∈N*,an>0,数列{an}的前n项和为Sn,且满足an+1=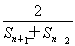 .
.
(1)求{Sn}的通项公式;
(2)设{bk}是{Sn}中的按从小到大顺序组成的整数数列.
①求b3;
②存在N(N∈N*),当n≤N时,使得在{Sn}中,数列{bk}有且只有20项,求N的范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(解析版) 题型:填空题
根据市场调查结果,预测某种家用商品从年初开始的n个月内累积的需求量Sn(万件)近似地满足关系式Sn=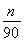 (21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________.
(21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(解析版) 题型:解答题
已知等差数列{an}满足:an+1>an(n∈N*),a1=1,该数列的前三项分别加上1,1,3后顺次成为等比数列{bn}的前三项.
(1)分别求数列{an}、{bn}的通项公式;
(2)设Tn= (n∈N*),若Tn+
(n∈N*),若Tn+ <c(c∈Z)恒成立,求c的最小值.
<c(c∈Z)恒成立,求c的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第4课时练习卷(解析版) 题型:解答题
已知数列{an}的前n项和为Sn,对一切正整数n,点Pn(n,Sn)都在函数f(x)=x2+2x的图象上,且在点Pn(n,Sn)处的切线的斜率为kn.
(1)求数列{an}的通项公式;
(2)若bn=2knan,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(解析版) 题型:解答题
已知数列{an}的首项a1=2a+1(a是常数,且a≠-1),
an=2an-1+n2-4n+2(n≥2),数列{bn}的首项b1=a,
bn=an+n2(n≥2).
(1)证明:{bn}从第2项起是以2为公比的等比数列;
(2)设Sn为数列{bn}的前n项和,且{Sn}是等比数列,求实数a的值;
(3)当a>0时,求数列{an}的最小项.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第1课时练习卷(解析版) 题型:解答题
若数列{an}满足an+1=an+an+2(n∈N*),则称数列{an}为“凸数列”.
(1)设数列{an}为“凸数列”,若a1=1,a2=-2,试写出该数列的前6项,并求出前6项之和;
(2)在“凸数列”{an}中,求证:an+3=-an,n∈N*;
(3)设a1=a,a2=b,若数列{an}为“凸数列”,求数列前2011项和S2011.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com