
已知数列{an}的首项a1=2a+1(a是常数,且a≠-1),
an=2an-1+n2-4n+2(n≥2),数列{bn}的首项b1=a,
bn=an+n2(n≥2).
(1)证明:{bn}从第2项起是以2为公比的等比数列;
(2)设Sn为数列{bn}的前n项和,且{Sn}是等比数列,求实数a的值;
(3)当a>0时,求数列{an}的最小项.
(1)见解析(2)a=-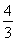 (3)当a∈
(3)当a∈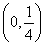 时,最小项为8a-1;当a=
时,最小项为8a-1;当a=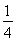 时,最小项为4a或8a-1;当a∈
时,最小项为4a或8a-1;当a∈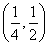 时,最小项为4a;当a=
时,最小项为4a;当a=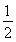 时,最小项为4a或2a+1;
时,最小项为4a或2a+1;
当a∈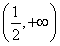 时,最小项为2a+1.
时,最小项为2a+1.
【解析】(1)证明:∵bn=an+n2,∴bn+1=an+1+(n+1)2=2an+(n+1)2-4(n+1)+2+(n+1)2=2an+2n2=2bn(n≥2).
由a1=2a+1,得a2=4a,b2=a2+4=4a+4,∵a≠-1,
∴b2≠0,即{bn}从第2项起是以2为公比的等比数列.
(2)【解析】
由(1)知bn=
Sn=a+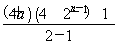 =-3a-4+(2a+2)2n,当n≥2时,
=-3a-4+(2a+2)2n,当n≥2时,
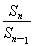 =
=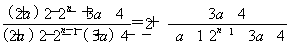 .
.
∵{Sn}是等比数列,∴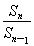 (n≥2)是常数,∴3a+4=0,即a=-
(n≥2)是常数,∴3a+4=0,即a=-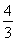 .
.
(3)【解析】
由(1)知当n≥2时,bn=(4a+4)2n-2=(a+1)2n,
∴an=
∴数列{an}为2a+1,4a,8a-1,16a,32a+7,…
显然最小项是前三项中的一项.
当a∈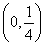 时,最小项为8a-1;当a=
时,最小项为8a-1;当a=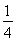 时,最小项为4a或8a-1;
时,最小项为4a或8a-1;
当a∈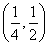 时,最小项为4a;当a=
时,最小项为4a;当a=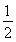 时,最小项为4a或2a+1;
时,最小项为4a或2a+1;
当a∈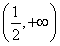 时,最小项为2a+1.
时,最小项为2a+1.


科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第2课时练习卷(解析版) 题型:填空题
过直线l外一点P,作与l平行的平面,则这样的平面有________个.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(解析版) 题型:解答题
已知数列{an}前n项和为Sn,且a2an=S2+Sn对一切正整数都成立.
(1)求a1,a2的值;
(2)设a1>0,数列 前n项和为Tn,当n为何值时,Tn最大?并求出最大值.
前n项和为Tn,当n为何值时,Tn最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第4课时练习卷(解析版) 题型:解答题
在各项均为正数的等比数列{an}中,已知a2=2a1+3,且3a2,a4,5a3成等差数列.
(1)求数列{an}的通项公式;
(2)设bn=log3an,求数列{anbn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(解析版) 题型:填空题
等比数列{an}的前n项和为Sn,已知S3=a2+10a1,a5=9,则a1=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第3课时练习卷(解析版) 题型:解答题
在数列{an}中,a1=2,an+1=4an-3n+1,n∈N*.
(1)求证:数列{an-n}是等比数列;
(2)求数列{an}的前n项和Sn;
(3)求证:不等式Sn+1≤4Sn对任意n∈N*皆成立.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第2课时练习卷(解析版) 题型:解答题
已知等差数列{an}的前n项和为Sn,n∈N*,且满足a2+a4=14,S7=70.
(1)求数列{an}的通项公式;
(2)若bn=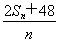 ,则数列{bn}的最小项是第几项,并求该项的值.
,则数列{bn}的最小项是第几项,并求该项的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com