练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在各项均为正数的等比数列{an}中，已知a2＝2a1＋3，且3a2，a4，5a3成等差数列．

    (1)求数列{an}的通项公式；

    (2)设bn＝log3an，求数列{anbn}的前n项和Sn.

     

    （1）3n，n∈N（2）Sn＝

    【解析】(1)设{an}公比为q，由题意得q>0，

    且解得 (舍)，

    所以数列{an}的通项公式为an＝3·3n－1＝3n，n∈N?．

    (2)由(1)可得bn＝log3an＝n，所以anbn＝n·3n.

    所以Sn＝1·3＋2·32＋3·33＋…＋n·3n，

    所以3Sn＝1·32＋2·33＋3·34＋…＋n·3n＋1，

    两式相减得，2Sn＝－3－(32＋33＋…＋3n)＋n·3n＋1＝－(3＋32＋33＋…＋3n)＋n·3n＋1＝－＋n·3n＋1＝，

    所以数列{anbn}的前n项和Sn＝.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第八章第2课时练习卷（解析版） 题型：填空题

    若m，n为两条不重合的直线，α，β为两个不重合的平面，则下列命题是真命题的是________．(填序号)

    ①若m、n都平行于平面α，则m、n一定不是相交直线；

    ②若m、n都垂直于平面α，则m、n一定是平行直线；

    ③已知α、β互相平行，m、n互相平行，若m∥α，则n∥β；

    ④若m、n在平面α内的射影互相平行，则m、n互相平行．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第6课时练习卷（解析版） 题型：解答题

    已知数列{an}中，a1＝2，n∈N*，an＞0，数列{an}的前n项和为Sn，且满足an＋1＝.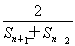

    (1)求{Sn}的通项公式；

    (2)设{bk}是{Sn}中的按从小到大顺序组成的整数数列．

    ①求b3；

    ②存在N(N∈N*)，当n≤N时，使得在{Sn}中，数列{bk}有且只有20项，求N的范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第5课时练习卷（解析版） 题型：解答题

    已知等差数列{an}满足：an＋1>an(n∈N*)，a1＝1，该数列的前三项分别加上1，1，3后顺次成为等比数列{bn}的前三项．

    (1)分别求数列{an}、{bn}的通项公式；

    (2)设Tn＝(n∈N*)，若Tn＋<c(c∈Z)恒成立，求c的最小值．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第4课时练习卷（解析版） 题型：解答题

    已知数列{an}的前n项和为Sn，对一切正整数n，点Pn(n，Sn)都在函数f(x)＝x2＋2x的图象上，且在点Pn(n，Sn)处的切线的斜率为kn.

    (1)求数列{an}的通项公式；

    (2)若bn＝2knan，求数列{bn}的前n项和Tn.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第4课时练习卷（解析版） 题型：解答题

    已知an＝

    (1)求数列{an}的前10项和S10；

    (2)求数列{an}的前2k项和S2k.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第3课时练习卷（解析版） 题型：解答题

    已知数列{an}的首项a1＝2a＋1(a是常数，且a≠－1)，

    an＝2an－1＋n2－4n＋2(n≥2)，数列{bn}的首项b1＝a，

    bn＝an＋n2(n≥2)．

    (1)证明：{bn}从第2项起是以2为公比的等比数列；

    (2)设Sn为数列{bn}的前n项和，且{Sn}是等比数列，求实数a的值；

    (3)当a>0时，求数列{an}的最小项．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第3课时练习卷（解析版） 题型：填空题

    等比数列{an}中，a1>0，a2a4＋2a3a5＋a4a6＝36，则a3＋a5＝________．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第二章第9课时练习卷（解析版） 题型：填空题

    若函数f(x)＝log2|ax－1|(a＞0)，当x≠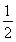时，有f(x)＝f(1－x)，则a＝________．

     

    查看答案和解析>>

    同步练习册答案