
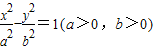 的右准线l2与一条渐近线l交于点P,F是双曲线的右焦点.
的右准线l2与一条渐近线l交于点P,F是双曲线的右焦点.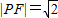 ,且双曲线的离心率
,且双曲线的离心率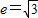 ,求该双曲线的方程;
,求该双曲线的方程;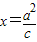 ,由对称性,不妨设渐近线l为
,由对称性,不妨设渐近线l为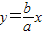 ,则
,则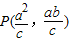 .
.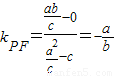 .
. ,∴
,∴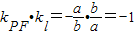 ,∴PF⊥l;
,∴PF⊥l;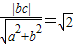 ,即b=
,即b=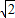 .
.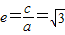 ,∴
,∴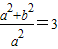 ,解得a2=1.
,解得a2=1.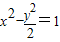 ;
;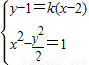 ,
,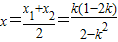 (1)
(1)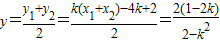 (2)
(2)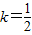 时,此时M(0,0).
时,此时M(0,0).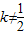 时,显然y≠0.此时(1)÷(2)得
时,显然y≠0.此时(1)÷(2)得 ,将其代入(2),
,将其代入(2), .∵y≠0,∴有2x2-y2-4x+y=0.显然(0,0)也满足此方程.
.∵y≠0,∴有2x2-y2-4x+y=0.显然(0,0)也满足此方程.

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 3 |
| PS |
| QS |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,一条渐近线方程是
,一条渐近线方程是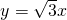 ,线段PQ是过曲线C右焦点F的一条弦,R是弦PQ的中点.
,线段PQ是过曲线C右焦点F的一条弦,R是弦PQ的中点.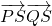 =0.当点P在曲线C上运动时,求a的取值范围.
=0.当点P在曲线C上运动时,求a的取值范围.查看答案和解析>>
科目:高中数学 来源:2012年广西南宁市高三第一次适应性测试数学试卷(理科)(解析版) 题型:解答题
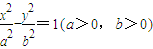 的右焦点为F,右准线为l,离心率为
的右焦点为F,右准线为l,离心率为 ,过y轴上一点A(0,b)作AM⊥l,垂足为M,则直线FM的斜率为 .
,过y轴上一点A(0,b)作AM⊥l,垂足为M,则直线FM的斜率为 .查看答案和解析>>
科目:高中数学 来源:2010年四川省资阳市高考数学三模试卷(理科)(解析版) 题型:解答题
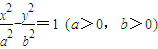 的右准线交x轴于A,虚轴的下端点为B,过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于P,过点A、B的直线与FP相交于点D,且
的右准线交x轴于A,虚轴的下端点为B,过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于P,过点A、B的直线与FP相交于点D,且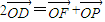 (O为坐标原点).
(O为坐标原点).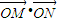 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com