
【题目】经济学中,函数f(x)的边际函数M(x)定义为M(x)=f(x+1)﹣f(x),利润函数p(x)边际利润函数定义为M1(x)=p(x+1)﹣p(x),某公司最多生产 100 台报系统装置,生产x台的收入函数为R(x)=3000x﹣20x2(单位:元),其成本函数为C(x)=500x+4000x(单位:元),利润是收入与成本之差.
(1)求利润函数p(x)及边际利润函数M1(x);
(2)利润函数p(x)与边际利润函数M1(x)是否具有相等的最大值?
【答案】
(1)解:P(x)=R(x)﹣C(x)=3000x﹣20x2﹣(500x+4000)
=﹣20x2+2500x﹣4000(1≤x≤100,x∈N*),
M1(x)=P(x+1)﹣P(x)=2480﹣40x.(1≤x≤100,x∈N*)
(2)解:∵P(x)=﹣20 ![]() +74125,
+74125,
∴当x=62 或63 时,P(x)max=74120.
又∵M1(x) 是减函数,∴当 x=1 时,M1(x)max=2440.
故利润函数p(x)与边际利润函数M1(x)不具有相等的最大值
【解析】(1)P(x)=R(x)﹣C(x),M1(x)=P(x+1)﹣P(x).(1≤x≤100,x∈N*).(2)由P(x)=﹣20 ![]() +74125,利用二次函数的单调性可得,P(x)max . 利用一次函数的单调性可得M1(x)max .
+74125,利用二次函数的单调性可得,P(x)max . 利用一次函数的单调性可得M1(x)max .


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:
【题目】已知10件不同产品中共有4件次品,现对它们进行一一测试,直至找到所有次品为止.
(1)若恰在第5次测试,才测试到第一件次品,第10次才找到最后一件次品的不同测试方法数有多少种?
(2)若恰在第5次测试后,就找出了所有次品,则这样的不同测试方法数有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上,点A、C为射线PM上的两点,点B、D为射线PN上两点,则有![]() (其中S△PAB、S△PCD分别为△PAB、△PCD的面积);空间中,点A、C为射线PM上的两点,点B、D为射线PN上的两点,点E、F为射线PL上的两点,则有
(其中S△PAB、S△PCD分别为△PAB、△PCD的面积);空间中,点A、C为射线PM上的两点,点B、D为射线PN上的两点,点E、F为射线PL上的两点,则有![]() =___________.(其中VP-ABE、VP-CDF分别为四面体P-ABE、P-CDF的体积)。
=___________.(其中VP-ABE、VP-CDF分别为四面体P-ABE、P-CDF的体积)。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=(x2﹣3)ex , 当m在R上变化时,设关于x的方程f2(x)﹣mf(x)﹣ ![]() =0的不同实数解的个数为n,则n的所有可能的值为( )
=0的不同实数解的个数为n,则n的所有可能的值为( )
A.3
B.1或3
C.3或5
D.1或3或5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 与
与![]() 的中心在原点,焦点分别在
的中心在原点,焦点分别在![]() 轴与
轴与![]() 轴上,它们有相同的离心率
轴上,它们有相同的离心率![]() ,并且
,并且![]() 的短轴为
的短轴为![]() 的长轴,
的长轴,![]() 与
与![]() 的四个焦点构成的四边形面积是
的四个焦点构成的四边形面积是![]() .
.
(1)求椭圆![]() 与
与![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 上非顶点的动点,
上非顶点的动点,![]() 与椭圆
与椭圆![]() 长轴两个顶点
长轴两个顶点![]() ,
,![]() 的连线
的连线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() ,
,![]() 点.
点.
(i)求证:直线![]() ,
,![]() 斜率之积为常数;
斜率之积为常数;
(ii)直线![]() 与直线
与直线![]() 的斜率之积是否为常数?若是,求出该值;若不是,说明理由.
的斜率之积是否为常数?若是,求出该值;若不是,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,其反函数为y=g(x).
,其反函数为y=g(x).
(1)若g(mx2+2x+1)的定义域为R,求实数m的取值范围;
(2)当x∈[﹣1,1]时,求函数y=[f(x)]2﹣2af(x)+3的最小值h(a);
(3)是否存在实数m>n>2,使得函数y=h(x)的定义域为[n,m],值域为[n2 , m2],若存在,求出m、n的值;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至11月份销售某种机械配件的销售量及销售单价进行了调查,销售单价x元和销售量y件之间的一组数据如表所示:
月份 | 7 | 8 | 9 | 10 | 11 |
销售单价x元 | 9 | 9.5 | 10 | 10.5 | 11 |
销售量y件 | 11 | 10 | 8 | 6 | 5 |
(1)根据7至11月份的数据,求出y关于x的回归直线方程;
(2)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润? 参考公式:回归直线方程 ![]() =b
=b ![]() +a,其中b=
+a,其中b= 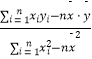 .
.
参考数据: ![]() =392,
=392, ![]() =502.5.
=502.5.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com