Question

6．为纪念中国抗日战争胜利70周年，某中学高三年级举办了“铭记历史，开创未来”的抗战历史知识竞赛活动，共有1000名学生参加了这次竞赛．为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计，请你根据频率分布表，解答下列问题：

序号	分组	频数	频率
1	[60，70）	①	0.15
2	[70，80）	20	0.2
3	[80，90）	35	0.35
4	[90，100）	30	②
合计		100	1

（1）写出频率分布表中①、②所代表的数据；
（2）在所给坐标系中画出样本的频率分布直方图；
（3）为鼓励更多的学生了解“抗战历史”知识，对成绩不低于90分的学生给予奖励，请估计在参加竞赛的1000名学生中大概有多少名学生获奖．

Answer 1

分析 （1）设频率分布表中①、②所代表的数据分别为x，y，由频率=$\frac{频数}{总数}$，能求出频率分布表中①、②所代表的数据．
（2）由频率分布表能画出样本的频率分布直方图．
（3）由频率分布表，得：成绩在[90，100）的学生的频率为0.3，由此能估计在参加竞赛的1000名学生中大概有多少名学生获奖．

解答 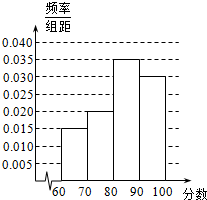解：（1）设频率分布表中①、②所代表的数据分别为x，y，
则由频率分布表得$\left\{\begin{array}{l}{\frac{x}{100}=0.15}\\{\frac{30}{100}=y}\end{array}\right.$，
解得x=15，y=0.3．
∴①为15，②为0.3．
（2）由频率分布表画出样本的频率分布直方图，如右图．
（3）由频率分布表，得：
成绩在[90，100）的学生的频率为0.3，
∴估计在参加竞赛的1000名学生中大概有：0.3×1000=300名学生获奖．

点评 本题考查频率分布直方图的应用，是基础题，解题时要认真审题，注意频率=$\frac{频数}{总数}$的灵活运用．