
分析 通过柯西不等式可知$\frac{{b}^{2}}{c}$+$\frac{{c}^{2}}{d}$+$\frac{{d}^{2}}{a}$≥$\frac{(b+c+d)^{2}}{c+d+a}$,利用a+b+c+d=4整理、拼凑可知$\frac{{a}^{2}}{b}$+$\frac{{b}^{2}}{c}$+$\frac{{c}^{2}}{d}$+$\frac{{d}^{2}}{a}$≥4+$\frac{4(a-b)^{2}}{b(4-b)}$,利用$\frac{4}{b(4-b)}$≥1整理即得结论.
解答 证明:$\frac{{a}^{2}}{b}$+$\frac{{b}^{2}}{c}$+$\frac{{c}^{2}}{d}$+$\frac{{d}^{2}}{a}$=$\frac{{a}^{2}}{b}$+($\frac{{b}^{2}}{c}$+$\frac{{c}^{2}}{d}$+$\frac{{d}^{2}}{a}$)
≥$\frac{{a}^{2}}{b}$+$\frac{(b+c+d)^{2}}{c+d+a}$(柯西不等式)
=$\frac{{a}^{2}}{b}$+$\frac{(4-a)^{2}}{4-b}$
=$\frac{(4-b){a}^{2}+b(4-a)^{2}}{b(4-b)}$
=$\frac{(16b-4{b}^{2})+(4{a}^{2}-8ab+4{b}^{2})}{b(4-b)}$
=4+$\frac{4(a-b)^{2}}{b(4-b)}$,
∵(b-2)2≥0,
∴$\frac{4}{b(4-b)}$≥1,
∴$\frac{4(a-b)^{2}}{b(4-b)}$≥(a-b)2,
∴$\frac{{a}^{2}}{b}$+$\frac{{b}^{2}}{c}$+$\frac{{c}^{2}}{d}$+$\frac{{d}^{2}}{a}$≥4+(a-b)2.
点评 本题考查不等式的证明,利用柯西不等式是解决本题的关键,注意解题方法的积累,属于中档题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:解答题
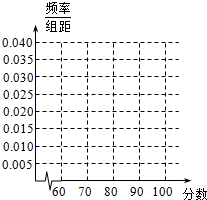 为纪念中国抗日战争胜利70周年,某中学高三年级举办了“铭记历史,开创未来”的抗战历史知识竞赛活动,共有1000名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,请你根据频率分布表,解答下列问题:
为纪念中国抗日战争胜利70周年,某中学高三年级举办了“铭记历史,开创未来”的抗战历史知识竞赛活动,共有1000名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,请你根据频率分布表,解答下列问题:| 序号 | 分组 | 频数 | 频率 |
| 1 | [60,70) | ① | 0.15 |
| 2 | [70,80) | 20 | 0.2 |
| 3 | [80,90) | 35 | 0.35 |
| 4 | [90,100) | 30 | ② |
| 合计 | 100 | 1 | |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某小区要建一个面积为500平方米的矩形绿地,四周有小路,绿地长边外路宽5米,短边外路宽8米,怎样设计绿地的长与宽,使绿地和小路所占的总面积最小,并求出最小值.
某小区要建一个面积为500平方米的矩形绿地,四周有小路,绿地长边外路宽5米,短边外路宽8米,怎样设计绿地的长与宽,使绿地和小路所占的总面积最小,并求出最小值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{5}$ | C. | $\frac{11}{5}$ | D. | $\frac{5}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com