
甲、乙、丙三人参加某项测试,他们能达标的概率分别是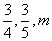 ,且三人能否达标互不影响.
,且三人能否达标互不影响.
(Ⅰ)若三人中至少有一人达标的概率是 ,求
,求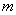 的值;
的值;
(Ⅱ)设甲在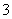 次相互独立的测试中能达标的次数为随机变量
次相互独立的测试中能达标的次数为随机变量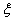 ,求
,求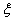 的概率分布列及数学期望.
的概率分布列及数学期望.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
为测树的高度,在水平地面上选取A、B两点(点A、B及树的底部在同一直线上),从A、B两点分别测得树尖的仰角为30°,45°,且A、B两点间的距离为60m,则树的高度为( )
A. 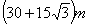 B.
B. 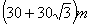 C.
C.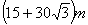 D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
已知命题p:函数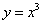 为R上的奇函数;命题q:若
为R上的奇函数;命题q:若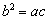 ,则a,b,c不一定成等比数列。下列说法正确的是
,则a,b,c不一定成等比数列。下列说法正确的是
A.p或q 为假 B.p且q 为真 C.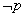 且q 为真 D.
且q 为真 D.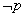 或q 为假
或q 为假
查看答案和解析>>
科目:高中数学 来源: 题型:
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,反设正确的是( )
A. 假设三内角都不大于60度
B. 假设三内角都大于60度
C. 假设三内角至多有一个大于60度
D. 假设三内角至多有两个大于60度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com