
分析 (Ⅰ)根据已知条件nSn+1-(n+3)Sn=0可以推知$\frac{{{S_{n+1}}}}{S_n}=\frac{n+3}{n}(n∈{{N}^*})$,且S1=a1=1;所以需要分类讨论:n=1和n≥2两种情况下的通项公式;
(Ⅱ)设${c_n}={(-1)^n}{b_n}={(-1)^n}{(n+1)^2}$,需要分类讨论:n为偶数和n为奇数两种情况.
解答 解:(Ⅰ)∵$\frac{{{S_{n+1}}}}{S_n}=\frac{n+3}{n}(n∈{{N}^*})$,且S1=a1=1,
∴当n≥2时,${S_n}={S_1}•\frac{S_2}{S_1}•\frac{S_3}{S_2}•…•\frac{S_n}{{{S_{n-1}}}}=1×\frac{4}{1}×\frac{5}{2}×\frac{6}{3}×…×\frac{n+2}{n-1}=\frac{n(n+1)(n+2)}{6}$,且S1=1也适合,
当n≥2时,${a_n}={S_n}-{S_{n-1}}=\frac{n(n+1)}{2}$,
且a1=1也适合,∴${a_n}=\frac{n(n+1)}{2}(n∈{{N}^*})$;
(Ⅱ)${b_n}={(n+1)^2}$.设${c_n}={(-1)^n}{b_n}={(-1)^n}{(n+1)^2}$,
当n为偶数时,∵${c_{n-1}}+{c_n}={(-1)^{n-1}}•{n^2}+{(-1)^n}•{(n+1)^2}=2n+1$,
∴${T_n}=({c_1}+{c_2})+({c_3}+{c_4})+…+({c_{n-1}}+{c_n})=5+9+13+…+(2n+1)=\frac{{\frac{n}{2}[5+(2n+1)]}}{2}=\frac{n(n+3)}{2}$.
当为奇数(n≥3)时,${T_n}={T_{n-1}}+{c_n}=\frac{(n-1)(n+2)}{2}-{(n+1)^2}=-\frac{{{n^2}+3n+4}}{2}$,
且T1=c1=-4也适合上式.
综上:得${T_n}=\left\{{\begin{array}{l}{-\frac{{{n^2}+3n+4}}{2}(n为奇数)}\\{\frac{n(n+3)}{2}(n为偶数)}\end{array}}\right.$.
点评 本题主要考查数列通项公式和前n项和的求解,利用累加法和分组求和法是解决本题的关键.


科目:高中数学 来源: 题型:解答题
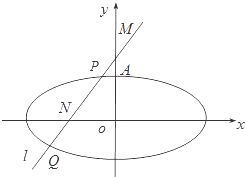 已知F1,F2,A分别为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点及上顶点△AF1F2的面积为4$\sqrt{3}$且椭圆的离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,4)的直线l与椭圆相交于不同的两点P、Q,点N在线段PQ上.
已知F1,F2,A分别为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点及上顶点△AF1F2的面积为4$\sqrt{3}$且椭圆的离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,4)的直线l与椭圆相交于不同的两点P、Q,点N在线段PQ上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 认为作业多 | 认为作业不多 | 合计 | |
| 喜欢玩手机游戏 | 18 | 2 | |
| 不喜欢玩手机游戏 | 6 | ||
| 合计 | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com