
分析 把直线的参数方程代入圆的方程可得:t2+$\sqrt{2}$t-4=0,可得直线被圆所截的弦长=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$.
解答 解:把直线$\left\{{\begin{array}{l}{x=2+\frac{{\sqrt{2}}}{2}t}\\{y=-1+\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$(t为参数)代入圆x2+y2=9可得:t2+$\sqrt{2}$t-4=0,
∴t1+t2=-$\sqrt{2}$,t1t2=-4.
∴直线被圆所截的弦长=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{2+4×4}$=3$\sqrt{2}$.
故答案为:$3\sqrt{2}$.
点评 本题考查了直线参数方程的应用、直线与圆相交弦长,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$±\sqrt{2}$x | B. | y=±2x | C. | y=±$\sqrt{3}$x | D. | y=±2$\sqrt{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
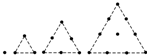 在古希腊,毕达哥拉斯学派把1,3,6,10,15,21,28,36,45,55,…这些数叫做三角形数,这是因为这些数目的点可以排成正三角形(如图所示),则三角形数的一般表达式f(n)=$\frac{n(n+1)}{2}$.
在古希腊,毕达哥拉斯学派把1,3,6,10,15,21,28,36,45,55,…这些数叫做三角形数,这是因为这些数目的点可以排成正三角形(如图所示),则三角形数的一般表达式f(n)=$\frac{n(n+1)}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | 3 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 性别 专业 | 非统计专业 | 统计专业 |
| 男 | 15 | 10 |
| 女 | 5 | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com