
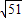
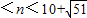
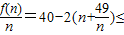 40-2×14=12,
40-2×14=12,

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用为12万元,以后每年都增加4万元,每年捕鱼收益50万元.
(1)问第几年开始获利?
(2)若干年后,有两种处理方案:
方案一:年平均获利最大时,以26万元出售该渔船
方案二:总纯收入获利最大时,以8万元出售该渔船.问哪种方案合算.
查看答案和解析>>
科目:高中数学 来源:2007年浙江省杭州市萧山区六八九三校高一期中联考尖子生数学竞赛试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com