
如图,P是平面四边形ABCD所在平面外一点,且AB=BC,AD=DC,PA=PC.
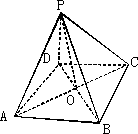
求证:平面PAC⊥平面PBD.
|
证明:设AC∩BD=O,连接PO. 因为AB=BC,AD=DC,BD=BD, 所以△ABD≌△CBD, 所以∠ADO=∠CDO. 易得△ADO≌△CDO. 所以OA=OC,即O为等腰三角 形ACD底边AC的中点, 则AC⊥BD. 又在△PAC中,PA=PC,OA=OC, 则AC⊥PO. 因为PO∩BD=O, 所以AC⊥平面PBD. 又AC 所以平面PAC⊥平面PBD. 寻线历程:证明α⊥β时,一般先在其中一个平面α(或β)内观察、寻找一条直线a,再判断直线a是否垂直于平面β(或α),然后运用面面垂直的判定定理即可得证.即将结论和条件相互结合,正推与逆推相结合即可解决问题. |


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
 如图,P是四边形ABCD所在平面外一点,O是AC与BD的交点,且PO⊥平面ABCD.当四边形ABCD满足下列条件
如图,P是四边形ABCD所在平面外一点,O是AC与BD的交点,且PO⊥平面ABCD.当四边形ABCD满足下列条件查看答案和解析>>
科目:高中数学 来源:2013届云南省芒市高二上学期期末考试数学试卷 题型:解答题
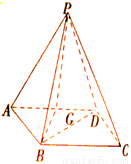
如图,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为 的菱形,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.若G为AD的中点,
的菱形,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.若G为AD的中点,
⑴求证:BG⊥平面PAD;
⑵求PB与面ABCD所成角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com