
【题目】已知函数![]() .
.
(I)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 和
和![]() 的值;
的值;
(II)讨论方程![]() 的解的个数,并说明理由.
的解的个数,并说明理由.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(I)求出![]() ,结合已知得到
,结合已知得到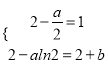 ,据此可求出
,据此可求出![]() 的值;(II)
的值;(II) ![]() 和
和![]() ,讨论求解,即可得到方程
,讨论求解,即可得到方程![]() 的解的个数,注意利用导数判断函数的单调性.
的解的个数,注意利用导数判断函数的单调性.
试题解析:(I)因为![]() ,
,
又![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,
,
所以![]() ,
,
解得![]() .
.
(II)当![]() 时,
时, ![]() 在定义域
在定义域![]() 内恒大于
内恒大于![]() ,此时方程无解.
,此时方程无解.
当![]() 时,
时, ![]() 在区间
在区间![]() 内恒成立,
内恒成立,
所以![]() 的定义域内为增函数.
的定义域内为增函数.
因为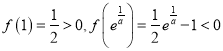 ,
,
所以方程有唯一解.
当![]() 时,
时, ![]() .
.
当![]() 时,
时, ![]() ,
,
![]() 在区间
在区间![]() 内为减函数,
内为减函数,
当![]() 时,
时, ![]() ,
,
![]() 在区间
在区间![]() 内为增函数,
内为增函数,
所以当![]() 时,
时,
取得最小值![]() .
.
当![]() 时,
时, ![]() ,无方程解;
,无方程解;
当![]() 时,
时, ![]() ,方程有唯一解.
,方程有唯一解.
当![]() 时,
时, ![]() ,
,
因为![]() ,且
,且![]() ,
,
所以方程![]() 在区间
在区间![]() 内有唯一解,
内有唯一解,
当![]() 时,
时,
设![]() ,
,
所以![]() 在区间
在区间![]() 内为增函数,
内为增函数,
又![]() ,所以
,所以![]() ,即
,即![]() ,
,
故![]() .
.
因为![]() ,
,
所以![]() .
.
所以方程![]() 在区间
在区间![]() 内有唯一解,
内有唯一解,
所以方程![]() 在区间
在区间![]() 内有两解,
内有两解,
综上所述,当![]() 时,方程无解,
时,方程无解,
当![]() ,或
,或![]() 时,方程有唯一解,
时,方程有唯一解,
当![]() 时,方程有两个解.
时,方程有两个解.


科目:高中数学 来源: 题型:
【题目】天气预报说,在今后的三天中,每一天下雨的概率均为40%.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨;再以每三个随机数作为一组,代表这三天的下雨情况.经随机模拟试验产生了如下20组随机数: 907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,这三天中恰有两天下雨的概率近似为( )
A.0.35
B.0.25
C.0.20
D.0.15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2 , 若对任意的x∈[t,t+2],不等式f(x+t)≥2f(x)恒成立,则实数t的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C的对边分别为a,b,c,且a>c,已知 ![]()
![]() =2,cosB=
=2,cosB= ![]() ,b=3,求:
,b=3,求:
(Ⅰ)a和c的值;
(Ⅱ)cos(B﹣C)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]()
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() 有两个极值点
有两个极值点![]() ,记过点
,记过点![]() 的直线的斜率为
的直线的斜率为![]() ,问:是否存在实数
,问:是否存在实数![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x﹣4.设圆C的半径为1,圆心在l上. 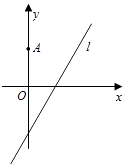
(1)若圆心C也在直线y=x﹣1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对应的边分别为a,b,c,且(2a﹣c)cosB=bcosC.
(Ⅰ)求角B的大小;
(Ⅱ)若cosA= ![]() ,a=2,求△ABC的面积.
,a=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10![]() cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(1)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com