
【题目】已知函数f(x)为定义在R上的奇函数,且当x>0时,f(x)=log3x,
(1)求f(x)的解析式;
(2)解不等式f(x)≤2.
【答案】
(1)解:易知f(0)=0;
当x<0时,则﹣x>0,所以f(x)=﹣f(﹣x)=﹣log3(﹣x);
所以f(x)= 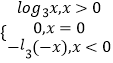
(2)解:由题意:当x>0时有log3x≤2,解得0<x≤9;
当x=0时,f(0)=0显然满足题意;
当x<0时有﹣log3(﹣x)≤2,即log3(﹣x)≥﹣2,解得 ![]() .
.
综上可得原不等式的解集为[0,9] ![]()
【解析】(1)根据函数为奇函数,可设x<0,则﹣x>0,然后将﹣x代入x>0时的解析式化简即可;(2)按照分段函数分段处理的原则列出不等式,分别解之,最终取并集即可.
【考点精析】掌握函数奇偶性的性质是解答本题的根本,需要知道在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


科目:高中数学 来源: 题型:
【题目】某网络营销部门为了统计某市网友2015年11月11日在某网店的网购情况,随机抽查了该市100名网友的网购金额情况,得到如下频率分布直方图.
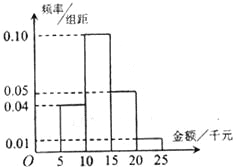
(1)估计直方图中网购金额的中位数;
(2)若规定网购金额超过15千元的顾客定义为“网购达人”,网购金额不超过15千元的顾客定义为“非网购达人”;若以该网店的频率估计全市“非网购达人”和“网购达人”的概率,从全市任意选取3人,则3人中“非网购达人”与“网购达人”的人数之差的绝对值为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=loga(ax+1)+mx是偶函数.
(1)求m;
(2)当a>1时,若函数f(x)的图像与直线l:y=﹣mx+n无公共点,求n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn . 已知a1=1, ![]() =an+1﹣
=an+1﹣ ![]() n2﹣n﹣
n2﹣n﹣ ![]() ,n∈N* .
,n∈N* .
(1)求数列{an}的通项公式;
(2)设数列{bn}满足an﹣an﹣1=bna ![]() ,求数列{bn}的n前项和Tn;
,求数列{bn}的n前项和Tn;
(3)是否存在实数λ,使得不等式λa ![]() ﹣
﹣ ![]() +a
+a ![]() +
+ ![]() ≥0恒成立,若存在,求出λ的取值范围;若不存在,请说明理由.
≥0恒成立,若存在,求出λ的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的短轴长为
的短轴长为![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于左、右顶点
上异于左、右顶点![]() 的一点.
的一点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,证明:点
,证明:点![]() 关于直线
关于直线![]() 的对称点在直线
的对称点在直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=x2+ax+3.
(1)当x∈R时,f(x)≥a恒成立,求a的取值范围.
(2)当x∈[﹣2,2]时,f(x)≥a恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sinxcosx+2cos2x﹣1(x∈R) (Ⅰ)求函数f(x)的最小正周期及在区间[0,
sinxcosx+2cos2x﹣1(x∈R) (Ⅰ)求函数f(x)的最小正周期及在区间[0, ![]() ]上的最大值和最小值;
]上的最大值和最小值;
(Ⅱ)若f(x0)= ![]() ,x0∈[
,x0∈[ ![]() ,
, ![]() ],求cos2x0的值.
],求cos2x0的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com